Revista Tecnología y Ciencia - Universidad Tecnológica Nacional
DOI:https://doi.org/10.33414/rtyc.38.83-103.2020 - ISSN 1666-6933
Reconocimiento-NoComercial 4.0 Internacional

Valoración Difusa de la Importancia Ambiental de las Acciones de Proyectos

Fuzzy Assessment of the Environmental Importance of Project Actions

Presentación: 15/02/2020

Aprobación: 27/05/2020

Susana LLAMAS

Facultad de Ingeniería, Universidad Nacional de Cuyo, Mendoza - Argentina

sllamas@uncuyo.edu.ar

Jorge BARÓN

Facultad de Ingeniería, Universidad Nacional de Cuyo, Mendoza - Argentina

jbaron@uncuyo.edu.ar

Resumen

Después de establecer la importancia del impacto ambiental de un proyecto se prepara el plan de gestión ambiental con los programas de vigilancia y control para las acciones más significativas y el programa de monitoreo para los factores ambientales más afectados. El programa de vigilancia y control contiene las medidas a implementar durante las etapas de construcción, funcionamiento y cierre del proyecto. El objetivo de este trabajo es, presentar un procedimiento metodológico de aplicación general que define un conjunto de atributos (aj) expresados por medio de variables lingüísticas a las que se les asignaron números, establece un indicador adimensional inicial para el cálculo de la Importancia de las Acciones del Proyecto (IAPj), emplea aritmética difusa para modelar la incertidumbre que se origina en la definición del conjunto de atributos (aj) y determina el valor final del indicador difuso por medio de los niveles de confianza (α) para proponer las medidas preventivas específicas en el programa de vigilancia y control ambiental.

Palabras clave: impacto ambiental, aritmética difusa, decisión multicriterio, acciones de proyecto

Abstract

After establishing the environmental impact importance of a project, the environmental management plan is prepared with the surveillance and control programs for the most significant actions and the monitoring program for the most affected environmental factors. The surveillance and control program contains the measures to be implemented during the construction, operation and closure stages of the project. The objective of this work is to present a methodological procedure of general application that defines a set of attributes (aj) expressed by means of linguistic variables to which numbers were assigned, establishes an initial dimensionless indicator for calculating the Importance of Project Actions (IPAj), uses fuzzy arithmetic to model the uncertainty that originates in the definition of the set of attributes (aj) and determines the final value of the fuzzy indicator by means of confidence levels (α) to propose specific preventive measures in the environmental monitoring and control program.

Keywords: environmental impact, fuzzy arithmetic, multicriteria decision, project actions

Introducción

La importancia del impacto ambiental de un proyecto es una medida cualitativa que se determina a partir de la definición de un conjunto de atributos, expresados por variables lingüísticas a las que se les asignan números, que valoran los impactos de las acciones del proyecto sobre los factores ambientales (Leopold et al. 1971, Conesa Fdez.-Vítora 1997, Garmendía et al. 2005, Conesa Fdez.-Vítora 2010, Gómez Orea 2010). Una vez determinada la importancia de cada impacto ambiental corresponde al proponente del proyecto confeccionar un plan de gestión ambiental integrado por dos programas: 1) El de vigilancia y control, con las medidas preventivas para las acciones más importantes del proyecto y 2) El de monitoreo, para el seguimiento de los factores ambientales más afectados. En consecuencia, es necesario que las medidas preventivas de vigilancia y control para las acciones del proyecto sean específicas, eficientes y verificables, ya que deben ser implementadas por el proponente y auditadas por la autoridad de control. Por otra parte, el programa de monitoreo sobre los factores ambientales dependerá, entre otros aspectos, de las recomendaciones de los expertos en cada factor, de las técnicas y del instrumental a utilizar, de la frecuencia de realización, de la idoneidad profesional del personal que los realiza y de la divulgación de sus resultados.

En una Evaluación de Impacto Ambiental (EIA) la descripción de las etapas de construcción, funcionamiento y cierre del proyecto se realiza para identificar las acciones que podrían causar impactos sobre los factores ambientales. Esta descripción se suele presentar en la forma de listas generales obtenidas de memorias técnicas más o menos exhaustivas según el estado de desarrollo del proyecto (por ejemplo: ingeniería conceptual, básica o de detalle). Sin embargo, diversos autores aconsejan que las acciones potencialmente impactantes del proyecto se ordenen en forma jerárquica en un árbol de acciones (Garmendía et al. 2005 p. 99, Conesa Fdez.-Vítora 2010 p. 229, Gómez Orea 2010 p. 298). Más recientemente se propuso que las acciones identificadas se ponderen según su importancia relativa en el proyecto (Llamas, et al. 2019, p. 51-70).

Si bien es abundante la cantidad de estudios que abordan la calidad de la valoración de la importancia de los impactos ambientales en las EIA (Thompson 1990, Barker et al. 1999, Goyal et al. 2001, Steinemann 2001, Enea et al. 2001, Zhao et al. 2006, Atkinson et al. 2006, Jay et al. 2007, Cloquell-Ballester et al. 2007, Peche et al. 2009, Tran et al. 2009, Cashmore et al. 2010, Hoyos 2010, Swor, et al. 2011, Bond et al. 2011, Pölönen et al. 2011, Morgan 2012, Zhang et al. 2013, Toro et al. 2013, Leung et al. 2015, Rahimi et al. 2015, Kang et al. 2016, Ji et al. 2016, Kågström 2016, Rathi 2017, Bond et al. 2016, Kamijo et al. 2017, Morgan 2017, Loomis et al. 2018, Kolhoff et al. 2018, Frini et al. 2019), no hay trabajos que describan qué criterios se deben considerar y de qué manera valorarlos para conocer la Importancia de las Acciones del Proyecto (IAP) en las etapas de construcción, funcionamiento y cierre. Sin embargo, en el procedimiento de EIA, esos criterios son elementos centrales para que los proyectos propuestos obtengan la Declaración de Impacto Ambiental (DIA); especialmente porque influyen en la valoración de las acciones del proyecto y en la preparación de las medidas preventivas que debe contener el programa de vigilancia y control ambiental.

Para facilitar el análisis de las acciones del proyecto desde las etapas iniciales de la EIA y promover la participación de los potenciales afectados por su ejecución, se pueden utilizar herramientas de decisión multicriterio (Saaty 1977, Saaty 1978, Canter 1982, Saaty 1987, Thompson 1990, Canter et al. 1993, Ramanathan 2001, Steinemann 2001, Janssen 2001, Zhao et al. 2006, Jay 2007, Hoyos 2010, Lin 2010, Huang 2011, Toro 2013, Stewart 2013, Leung 2015, Cardenas 2016, NG 2016, Rathi 2017, Loomis 2018, Llamas et al. 2019). Para tratar la información cualitativa, generalmente expresada por variables lingüísticas a las que se les asignan valores numéricos, el empleo de la lógica difusa por medio de la aritmética difusa, es una forma adecuada de representar el conocimiento aproximado y permite confeccionar un programa de vigilancia y control con medidas preventivas específicas para las acciones más significativas del proyecto (Zadeh 1965, Bellman et al. 1970, Zadeh 1971, Zadeh 1978, Dubois et al. 1980, Dubois et al. 1987, Klir et al. 1995, Parashar et al. 1997, Zadeh 1999, Dubois et al. 2000, Enea et al. 2001, Grzegorzewski 2002, Lin et al. 2010, Couso et al. 2010, Dubois 2011, Peche et al. 2009, Li et al. 2014).

El objetivo de este trabajo es, presentar un procedimiento metodológico de uso general que define atributos (aj) para la valoración de la Importancia de las acciones del Proyecto (IAPj), aplicar el análisis multicriterio discreto, por medio del Proceso Analítico Jerárquico (AHP: Analytic Hierarchy Process), para ordenar los criterios de decisión realizando comparaciones por pares, desarrollar una expresión polinómica adimensional específica para calificar la Importancia de las Acciones del Proyecto (IAPj), utilizar la aritmética difusa para modelar la incertidumbre que se origina en la definición de un conjunto de atributos (aj) expresados por medio de variables lingüísticas a las que se les asignan números, determinar los estimadores centrales y los intervalos de confianza asociados por medio de niveles de confianza (α) y proponer medidas preventivas específicas para el programa de vigilancia y control ambiental.

Definición de atributos, variables lingüísticas y coeficientes (aj)

El conjunto de atributos, variables lingüísticas y coeficientes (aj), definidos para calcular el valor de la Importancia de las Acciones de Proyecto (IAPj), se presenta en la Tabla 1.

Tabla 1. Valoración de los atributos para el cálculo de la IAP. Elaboración propia

Realizando la suma polinómica de los valores mínimos y máximos de cada atributo se obtienen los extremos de variación: 180 ≤ IAP ≤ 570. Estos valores se obtuvieron sumando coeficientes (aj) con diferentes unidades de medida y escalas, por lo que, para obtener la expresión adimensional de la IAPj, se recurrió al análisis multicriterio discreto utilizando el Proceso Analítico Jerárquico (AHP: Analytic Hierarchy Process) que emplea matrices de comparaciones por pares de criterios (Saaty 1977, Saaty 1978, Saaty 1987, Saayt 2008).

Valoración adimensional inicial de la IAPj

Para obtener la valoración adimensional inicial (clásica o crisp) de la Importancia de las Acciones del Proyecto (IAPj) fue necesario calcular el peso relativo (ws), con el que cada atributo (aj) participa del cálculo, a partir de la confección de una matriz de comparación por pares de atributos.

Se recurrió al método Delphi de convergencia (Landeta 1999, Villarreal Larrinaga et al. 2010, Reguant-Álvarez et al. 2016) que tiene en cuenta las valoraciones otorgadas a la importancia de los atributos (aj) por medio de la realización de encuestas al panel de expertos extraídos de los diferentes grupos con interés en el proyecto (Conesa Fdez.-Vítora 2010, p. 261-263, Llamas et al. 2019). Los integrantes del panel de expertos reciben un cuestionario que deben responder asignando un valor a la intensidad de importancia de cada atributo (aj), según la escala fundamental de números absolutos propuesta por Saaty (1977, p. 246), que se presenta en la Tabla 2. Para completar una nueva ronda de consultas cada integrante del panel de expertos recibe las valoraciones realizadas por el resto de los panelistas y regresa su respuesta. El proceso se repite hasta lograr la convergencia de las valoraciones recibidas.

Intensidad de importancia en una escala absoluta

Definición

Explicación

1

Igual importancia

Dos actividades contribuyen igual al objetivo

3

Importancia moderada de uno respecto del otro

La experiencia y el juicio favorecen una actividad sobre otra

5

Importancia esencial o fuerte

La experiencia y el juicio favorecen más una actividad sobre otra

7

Importancia muy fuerte

Una actividad está fuertemente favorecida y su dominio demostrado en la práctica

9

Importancia extrema

La evidencia a favor de una actividad sobre otra corresponde al mayor orden posible de afirmación

2, 4, 6, 8

Valores intermedios entre las dos sentencias adyacentes

Cuando se necesita compromiso entre los valores anteriores

Recíprocas

Si la actividad i tiene uno de los números anteriores que se le asignen en comparación con la actividad j, entonces j tiene el valor inverso en comparación con i

Racionales

Ratios derivados de la escala

Si la consistencia tuviese que ser forzada por la obtención de n valores numéricos para abarcar la matriz

Tabla 2. Escala fundamental de preferencias. Fuente: Saaty 1977, p. 246

Con las valoraciones realizadas por el panel de expertos se confeccionó la matriz de comparación por pares de atributos (aj), presentada en la Tabla 3, que cumple las siguientes condiciones algebraicas: cuadrada ; positiva: ; recíproca: ; con elementos diagonales iguales a uno: y consistente: (Saaty 1977, p. 244-251, Saaty 1987, p. 172).

Área de influencia (AI)

Ubicación (UB)

Extensión (EX)

Momento (MO)

Persistencia (PE)

Reversibilidad (RE)

Recuperabilidad (RC)

Entradas (EN)

Salidas (SL)

Trabajo (TR)

Área de influencia (AI)

1

1

1

1

1

1

1

1/7

1/5

1/3

Ubicación (UB)

1

1

1

1

1

1

1

1/7

1/5

1/3

Extensión (EX)

1

1

1

1

1

1

1

1/7

1/5

1/3

Momento (MO)

1

1

1

1

1

1

1

1/7

1/5

1/3

Persistencia (PE)

1

1

1

1

1

1

1

1/7

1/5

1/3

Reversibilidad (RE)

1

1

1

1

1

1

1

1/7

1/5

1/3

Recuperabilidad (RC)

1

1

1

1

1

1

1

1/7

1/5

1/3

Entradas (EN)

7

7

7

7

7

7

7

1

1

3

Salidas (SL)

5

5

5

5

5

5

5

1

1

1

Trabajo (TR)

3

3

3

3

3

3

3

1/3

1

1

SUMA

22.00

22.00

22.00

22.00

22.00

22.00

22.00

3.33

4.40

7.33

Tabla 3. Matriz de comparación por pares de atributos (aj). Elaboración propia

La consistencia de la matriz de comparación por pares de atributos (aj) se comprueba obteniendo el principal valor propio (λmax), necesario para calcular el índice de consistencia aleatoria IC = (λmax-n)/(n-1). A continuación, se obtiene la relación de consistencia RC = IC/Índice aleatorio, donde el Índice aleatorio depende del tamaño (n) de la matriz de comparación por pares de atributos y cuyos valores se presentan en la Tabla 4. Finalmente se verifica que el IC resulte inferior al 10 % recomendado por el autor del método (Saaty 1977, p. 244-251, Saaty 1987, p. 172).

n

1

2

3

4

5

6

7

8

9

10

Índice aleatorio

0

0

0.58

0.90

1.12

1.24

1.32

1.41

1.45

1.49

Tabla 4. Índice promedio de consistencia aleatorio. Fuente: Saaty 1977, p. 244-251, Saaty 1987, p. 171

El AHP requiere sumar los valores de cada columna de la Tabla 3 y realizar el cociente entre el valor de cada celda y el de la suma de la columna correspondiente para obtener la matriz de comparación por pares de atributos (aj) normalizada, que se presenta en la Tabla 5. A continuación, se agrega una nueva columna con los valores de la suma de sus filas y luego se suman los valores de dicha columna.

 

AI

UB

EX

MO

PE

RE

RC

EN

SL

TR

Suma Filas

Vector Prioridad (ws)

Vector Propio

Cociente

Área de influencia (AI)

0,05

0,05

0,05

0,05

0,05

0,05

0,05

0,04

0,05

0,05

0,45

0,05

0,45

10,04

Ubicación (UB)

0,05

0,05

0,05

0,05

0,05

0,05

0,05

0,04

0,05

0,05

0,45

0,05

0,45

10,04

Extensión (EX)

0,05

0,05

0,05

0,05

0,05

0,05

0,05

0,04

0,05

0,05

0,45

0,05

0,45

10,04

Momento (MO)

0,05

0,05

0,05

0,05

0,05

0,05

0,05

0,04

0,05

0,05

0,45

0,05

0,45

10,04

Persistencia (PE)

0,05

0,05

0,05

0,05

0,05

0,05

0,05

0,04

0,05

0,05

0,45

0,05

0,45

10,04

Reversibilidad (RE)

0,05

0,05

0,05

0,05

0,05

0,05

0,05

0,04

0,05

0,05

0,45

0,05

0,45

10,04

Recuperabilidad (RC)

0,05

0,05

0,05

0,05

0,05

0,05

0,05

0,04

0,05

0,05

0,45

0,05

0,45

10,04

Entradas (EN)

0,32

0,32

0,32

0,32

0,32

0,32

0,32

0,30

0,23

0,41

3,16

0,32

3,18

10,06

Salidas (SL)

0,23

0,23

0,23

0,23

0,23

0,23

0,23

0,30

0,23

0,14

2,25

0,23

2,27

10,05

Trabajo (TR)

0,14

0,14

0,14

0,14

0,14

0,14

0,14

0,10

0,23

0,14

1,42

0,14

1,42

10,03

SUMA

1

1

1

1

1

1

1

1

1

1

10,00

10,05

Tabla 5. Matriz de comparación por pares de atributos (aj) normalizada. Elaboración propia

Para obtener el coeficiente (ws), que corresponde al Vector Prioridad presentado en la Tabla 5, se realiza el cociente entre cada valor de la columna identificada como Suma Filas y el total de la misma. Luego se realiza el producto matricial entre la matriz de comparación por pares de atributos (Tabla 3) y el Vector Prioridad (ws) de la Tabla 5 y se obtiene el principal Vector Propio. En la última columna de la Tabla 5 se ubican los valores correspondientes al cociente entre los valores del Vector Propio y los del Vector Prioridad (ws) para cada fila de la matriz normalizada. El principal Valor Propio de la matriz (λmax = 10.04) se obtiene promediando los valores de la última columna y la consistencia de la matriz se verifica calculando el Índice de consistencia aleatoria IC = (λmax-10)/(10-1) = 0.00. El cálculo de la relación de consistencia (RC) utiliza el Índice aleatorio, que depende del tamaño de la matriz (n), presentado en la Tabla 4, RC = IC/Índice aleatorio = 0.00/1.49 = 0.00 y se verifica que los valores obtenidos resulten inferiores al 10 % recomendado por el autor del método (Saaty 1987, p. 172).

Con la obtención de los coeficientes (ws), que acompañan a cada atributo (aj) definido para determinar la Importancia de las Acciones del Proyecto (IAPj), la suma de los valores mínimos y máximos presenta valores adimensionales, como queda expresado en la ecuación (1) que corresponde al polinomio algebraico desarrollado para el cálculo adimensional inicial (clásico o crisp) de la IAPj, válido para las etapas de construcción, funcionamiento y cierre del proyecto.

(1)

Utilizando la ecuación (1) se obtuvieron los valores adimensionales iniciales (clásicos o crisp) mínimo () y máximo () entre los cuales puede variar la IAPj.

Para determinar los rangos de variación intermedios entre los extremos posibles de la IAPj el método propuesto establece una calificación arbitraria pero no subjetiva, de manera tal que toda IAPj inferior a 13 unidades se considera de importancia baja y toda IAPj igual o superior a 30 se considera de importancia muy alta. Asimismo 22 IAPj se estableció como valor central para calificar la IAPj de importancia media (13 ≤ IAPj < 22) y de importancia alta (22 ≤ IAPj < 30).

Los intervalos adimensionales definidos entre los extremos para la calificación inicial (clásica o crisp) del indicador IAPj, son los reunidos en el conjunto de expresiones identificadas con el número (2).

IAPj < 13 BAJA

13 ≤ IAPj < 22 MEDIA (2)

22 ≤ IAPj < 30 ALTA

IAPj ≥ 30 MUY ALTA

El cálculo del indicador IAP, para cada acción del proyecto, se realiza aplicando la ecuación (1) y con base en los rangos de variación definidos en el conjunto de expresiones (2), se obtiene la calificación inicial (clásica o crisp) de la IAPj para las acciones del proyecto según las variables lingüísticas resultantes en: Baja. Media. Alta. Muy Alta.

Modelación de la incertidumbre con conjuntos difusos

La incertidumbre de los valores de los atributos (aj), definidos para modelar la Importancia de las Acciones del Proyecto (IAPj), se relaciona con la ignorancia que incluye el error de medición, la indecisión sobre la forma matemática del modelo y la confusión sobre el nivel apropiado de abstracción (Lin, et al. 2010). Esta incertidumbre se puede expresar como un intervalo de confianza que incluye una estimación de los límites inferior y superior (Juang et al. 1998, p. 112) y se representa por medio de un conjunto difuso, definido por un par ordenado , donde un elemento x pertenece al conjunto X, en un grado de la función de pertenencia que varía en [0, 1].

Una variable difusa en un conjunto difuso tiene, al menos, un valor en el que el grado de pertenencia es 1. Es decir que existe un único valor (Zadeh 1965, Bellman et al. 1970, Zadeh 1971, Dubois et al. 1987, Klir et al. 1995, Peche et al. 2009 p. 281).

Cuando el valor de un atributo (aj) se ubica dentro del intervalo de confianza la incertidumbre queda limitada, dado que el valor de aj pertenece a dicho intervalo. A cada intervalo se le asigna un nivel de presunción haciendo posible que los límites del intervalo cambien según el valor del nivel de presunción, como se puede ver en la Figura 1, para α´ y α.

Figura 1. Intervalo de confianza . Función de pertenencia para un número difuso triangular. Elaboración propia

Utilizando el exponente α para indicar el nivel de presunción del intervalo de confianza , resulta que, cuando α=0 el nivel de presunción para dicho intervalo es mínimo, cuando α=1 el nivel de presunción es máximo, mientras que para valores entre 0 y 1 el nivel de presunción variará entre el mínimo y el máximo (Klir et al. 1995, 97-102). En la Figura 1 se observa que la variación del nivel de presunción α queda representada por el segmento ascendente (left) de la función de pertenencia respecto de y por el segmento descendente (right) para (Li et al. 2014). Esto queda expresado en la ecuación (3) de la siguiente manera:

(3)

La transformación de las variables lingüísticas se realizó empleando aritmética difusa para representarlas por medio de números difusos triangulares unimodales. Para hacerlo se emplearon funciones de forma del tipo l (left) - r (right) representadas por sus intervalos de confianza asociados , que son una generalización del concepto de número difuso y permiten expresar funciones de pertenencia en su forma equivalente (Dubois et al. 1980 p. 53, Kaufmann et al. 1985, Dubois et al. 2004).

Se adoptó la representación triangular del número difuso , donde es el valor central (modal) del intervalo de confianza cuando α=1.

Para un atributo aj la incertidumbre está limitada entre los valores extremos del intervalo de confianza considerado y, por medio de la representación triangular de la función de pertenencia , queda determinada con las siguientes expresiones:

(4)

(5)

(6)

(7)

Donde, en el intervalo de confianza mencionado: = valor inicial (left) para α=0, = valor central (modal) para α=1 y = valor final (right) para α=0.

Utilizando la forma alternativa de definir un número difuso triangular, por medio de su intervalo de confianza, de las expresiones (5) y (6), se despeja el valor del atributo aj y se hacen las siguientes sustituciones:

,,, para obtener las expresiones (8) y (9).

(8)

(9)

La expresión del intervalo de confianza generalizado queda representada por la ecuación (10).

(10)

Para tener en cuenta la contribución de cada atributo (aj) a la IAPj se adoptó un valor (v), calculado a partir de una función de evaluación , que tiene en cuenta el sentido creciente o decreciente de dicha contribución a partir de la definición de una función de evaluación parabólica creciente y una función parabólica decreciente , respectivamente.

Procedimiento de valoración difusa de la Importancia de las Acciones del Proyecto

( )

A continuación, se presenta el procedimiento desarrollado para valorar la Importancia de las Acciones del Proyecto () con aritmética difusa, explicado con ejemplos ilustrativos.

Valoración difusa de los atributos ()

Los rangos propuestos para la valoración inicial (clásica o crisp) de la IAPj, que se calcula con la ecuación (1), presentan límites rígidos. Por ejemplo, según el conjunto de expresiones (2), una acción con una IAPj = 21 debe ser calificada como de importancia Media. Sin embargo, ese valor está más cerca del extremo superior del rango [13 ≤ IAPj < 22) y con la calificación inicial (crisp) obtenida la importancia de esa acción podría resultar subestimada.

Para explicar con un ejemplo la valoración difusa de los atributos (aj) definidos en la Tabla 1, se presenta el cálculo del atributo Extensión (EXj) que se describió utilizando las tres variables lingüísticas definidas y los valores numéricos asociados a cada una: Baja < 5% = 10. Media (entre 5% y 35%) = 20. Grande (entre 35% y 75%) = 30.

Empleando la expresión (10) se construye el intervalo de confianza para el atributo Extensión (EXj), con = 10, =20 y =30. Utilizando una función parabólica creciente con = , se obtuvo la contribución para la valoración de la en el intervalo [10, 30], cuyos valores se presentan en la Tabla 6 y se grafican en la Figura 2.

Tabla 6. Valores difusos del atributo Extensión (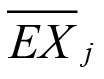). Elaboración propia

Figura 2. Representación difusa del atributo Extensión (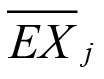). Elaboración propia

El procedimiento de valoración difusa es el mismo para todos los atributos (aj) definidos en la Tabla 1.

Valoración difusa de la

El cálculo del valor inicial (clásico o crisp) de la IAPj se realiza utilizando la ecuación (1). Los valores intermedios posibles entr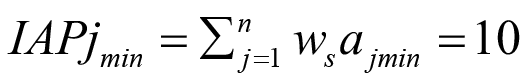e e 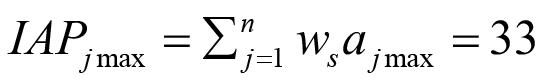, representados por las variables lingüísticas (Baja. Media. Alta. Muy Alta) se calcularon utilizando aritmética difusa (Zadeh 1965, Bellman et al. 1970, Zadeh 1978, Zadeh 1983, Dubois et al. 1987). Las funciones de pertenencia triangulares se definieron empleando funciones de forma l (left) y r (right) para representarlas por sus intervalos de confianza asociados .

Cada número difuso triangular quedó representado por el valor central (modal) y su intervalo de confianza asociado [0,1] empleando la ecuación (10), reescrita en la ecuación (11) para representar la .

(11)

Donde: = 10 (rama ascendente por la izquierda-left); = 33 (rama descendente por la derecha-right); = 22 (valor central, modal).

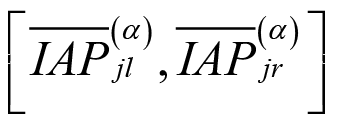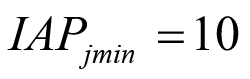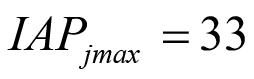El número difuso triangular definido para representar al intervalo de calificación determinado entre e es 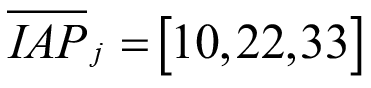y utilizando la ecuación (11) el desarrollo del α-corte, o nivel de presunción (α) resultante, es el siguiente 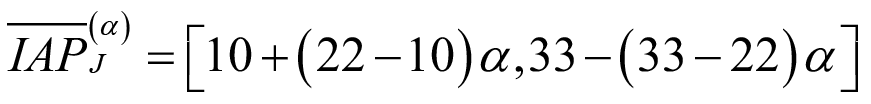.Con los valores obtenidos, que se presentan en la Tabla 7 y se grafican en la Figura 3, se comprueba que para 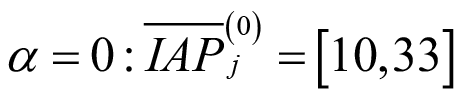y para .

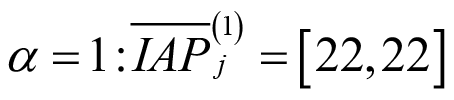Tabla 7. Intervalo de confianza [10, 33] y calificación para . Elaboración propia

La Figura 3 es la representación gráfica final de la que permite analizar las acciones de un proyecto según su valoración difusa, determinada por el estimador central (modal) y su intervalo de confianza asociado. Un breve análisis, realizado para dos valores de la IAPj, permite explicar la aplicación del procedimiento desarrollado.

Figura 3. Importancia difusa de las acciones de proyecto. Intervalos de calificación de la 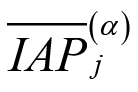. Elaboración propia

Una acción del proyecto con un valor inicial (clásico o crisp) IAP = 19, obtenido por aplicación de la expresión polinómica presentada en la ecuación (1), califica como de importancia Media en el rango definido en el conjunto de expresiones (2).

Sin embargo, al considerar el intervalo de calificación difuso de la , en la Figura 3 se puede advertir que la traza vertical del valor intercepta dos niveles de confianza diferentes según los puntos de corte. Es decir que, para una con un nivel de confianza α = 0,32 la calificación de la acción es de importancia Baja, pero para α = 0,68 se debe mantener la calificación de importancia Media. Esta confirmación de la calificación inicial de la se determina con base en el nivel de confianza más alto.

Por otra parte, una acción del proyecto con un valor inicial (clásico o crisp) de IAP = 28, calculada con la ecuación (1) y según el conjunto de expresiones (2), corresponde a una acción de importancia inicial Alta. Sin embargo, en la Figura 3 se puede comprobar que al trazar la vertical desde el valor de 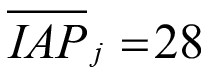, los dos niveles de confianza interceptados son α = 0,25 que corresponde a una importancia Alta y α = 0,75 que corresponde a una importancia Muy alta, con lo que se debe modificar la calificación inicial para expresarla como acción de importancia Muy alta.

Resultados

El procedimiento desarrollado se aplicó a la etapa de funcionamiento de un proyecto para la explotación de un yacimiento minero metalífero desarrollado a nivel de Ingeniería básica, situado en el sector central de la cordillera de Los Andes, en la provincia de Mendoza, República Argentina. En la descripción del proyecto se contabilizó un total de 11 acciones para la etapa de funcionamiento (Llamas, et al. 2019 p. 51-70).

El cálculo de la IAPj inicial (clásica o crisp) para las 11 acciones que componen la etapa de funcionamiento se realizó con datos obtenidos del proyecto1 , utilizando los atributos definidos en la Tabla 1 y con los coeficientes presentados en la ecuación (1), se obtuvieron los resultados que se muestran en la última columna de la Tabla 8.

>

Tabla 8. Etapa de funcionamiento. Importancia de Acciones de Proyecto. Elaboración propia

Utilizando la Figura 3, que representa los rangos para valorar la , se obtuvieron las calificaciones finales (difusas) de las acciones presentadas en la última columna de la Tabla 9.

La calificación inicial (clásica o crisp) de la IAPj para las 11 acciones de la etapa de funcionamiento del proyecto minero del ejemplo, expresadas con base en los rangos de calificación propuestos en el conjunto de expresiones (2), contabilizó 4 acciones de importancia Media y 7 de importancia Alta. Con estos resultados, el proponente del proyecto queda obligado a confeccionar un programa de vigilancia y control ambiental para cada una de las 11 acciones de la etapa de funcionamiento del proyecto.

Tabla 9. Importancia de Acciones de Proyecto, calificación inicial y difusa. Elaboración propia

Sin embargo, el valor final (difuso) de la 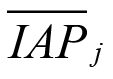incluido en la última columna de la Tabla 9 permite comprobar que, aplicando el procedimiento desarrollado para las 11 acciones de la etapa de funcionamiento del proyecto minero del ejemplo, ahora son 3 las acciones calificadas como de importancia Baja, 2 de importancia Media, 3 de importancia Alta y 3 de importancia Muy alta. Con estos resultados corresponde al proponente del proyecto elaborar el programa de vigilancia y control ambiental para 8 de las 11 acciones de la etapa de funcionamiento, como se explica a continuación.

Las medidas del programa de vigilancia y control se preparan a partir de las valoraciones difusas de los atributos 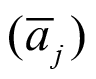definidos para valorar la 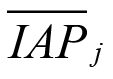de cada una de las acciones del proyecto: 1) Área de influencia. 2) Ubicación. 3) Extensión. 4) Momento. 5) Persistencia. 6) Reversibilidad. 7) Recuperabilidad. 8) Entradas. 9) Salidas. 10) Trabajo. De esta manera el control de cada acción de la etapa de funcionamiento del proyecto, se realiza con base en una valoración más rigurosa y verificable de cada atributo.

Con base en la calificación final (difusa) obtenida para cada 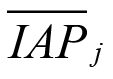, el proponente del proyecto debe precisar los requerimientos del programa de vigilancia y control para 3 acciones calificadas con importancia Muy Alta, 3 con importancia Alta y 2 con importancia Media, por medio de una descripción más precisa de los métodos y las técnicas de control a implementar, el tipo, cantidad, especificaciones y calidad de los instrumentos a utilizar, la frecuencia de las mediciones, la identificación y el grado de capacitación de cada responsable de realizar los controles, entre otros.

Para las 3 acciones calificadas con una importancia Baja el proponente del proyecto deberá explicar los procedimientos de control rutinarios que implementará para que esas 3 acciones de la etapa de funcionamiento del proyecto conserven la calificación obtenida.

Discusión

La significancia de los resultados presentados se manifiesta en la valoración de la Importancia de las Acciones del Proyecto (IAPj), a partir de un conjunto de atributos 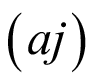bien definidos, que mejoran la preparación del programa de vigilancia y control para las acciones del proyecto, con medidas específicas según el valor final (difuso) del indicador .

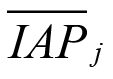La introducción de alguna modificación en el proyecto producirá un nuevo conjunto de acciones, cuyos atributos 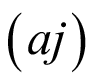también se pueden valorar con el procedimiento propuesto. Esta novedad fortalece la participación de los diferentes sectores de la sociedad en la revisión del proyecto propuesto, con la posibilidad de aportar sugerencias para compatibilizar las discrepancias técnicas, económicas, sociales y ambientales.

El análisis de las acciones del proyecto, a partir de un indicador específico como la IAPj, no había sido abordado en la abundante literatura existente. En particular, esta deficiencia se advierte en la etapa inicial de la Evaluación de Impacto Ambiental (EIA), cuando se realiza la descripción del proyecto y sus alternativas para identificar las acciones potencialmente impactantes.

Conclusiones

Con el procedimiento metodológico presentado se puso en evidencia la relevancia de calificar las acciones de un proyecto utilizando una expresión polinómica sencilla, que valora todos los atributos (aj) utilizando criterios jerarquizados por medio del peso relativo (ws), para calcular el indicador inicial (clásico o crisp) de la IAPj. La valoración final (difusa) del indicador 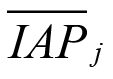, determinado por medio de sus intervalos de confianza, es la que permite ubicar el nivel de confianza (α) que determina la calificación más apropiada de cada acción del proyecto y de esa manera formalizar la presentación del plan de vigilancia y control para las acciones más significativas del proyecto.

La contribución novedosa del procedimiento propuesto consiste en la definición del conjunto de atributos (aj) para valorar las acciones de un proyecto, la obtención de una expresión polinómica adimensional para calcular la IAPj y la determinación de los estimadores puntuales y sus intervalos de confianza asociados definidos a partir de los niveles de confianza (α) por medio de la aplicación de la aritmética difusa.

Con relación al objetivo expresado, se concluye que ahora se dispone de un procedimiento metodológico de uso general, compuesto por un conjunto de atributos bien definidos, un polinomio algebraico adimensional específico para calificar las acciones de un proyecto con el indicador inicial (clásico o crisp) IAPj y una gráfica para la calificación final (difusa) de la 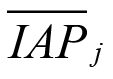que tiene en cuenta los niveles de confianza (α).

Referencias

Atkinson, S., Canter, L. W., Ravan, M.D. (2006). The influence of incomplete or unavailable information on environmental impact assessment in the USA. Environmental Impact Assessment Review 26. 448–467. DOI.org/10.1016/j.eiar.2006.01.001.

Barker, A., Wood, C. (1999). An Evaluation of EIA System Performance in Eight EU Countries. Environ Impact Assess Rev. 19:387–404. DOI.org/10.1016/S0195-9255(99)00015-3.

Bellman, R.E., Zadeh, L.A. (1970). Decision-Making in a Fuzzy Environment. Management Science. 17 (4), 141-164. DOI.10.1287/mnsc.17.4.B141.

Bond. A., Morrison-Saunders, A. (2011). Re-evaluating Sustainability Assessment: Aligning the vision and the practice. Environmental Impact Assessment Review. 31 (1), 1–7. DOI.10.1016/j.eiar.2010.01.007.

Bond, A., Pope, J., Morrison-Saunders, A., Retief, F. (2016). A game theory perspective on environmental assessment: What games are played and what does this tell us about decision making rationality and legitimacy? Environmental Impact Assessment Review 57. 187–194. DOI.org/10.1016/j.eiar.2016.01.002.

Canter, Larry W. (1982). Environmental Impact Assessment. Impact Assessment, 1:2, 6-40, DOI.10.1080/07349165.1982.9725447.

Canter, L. W., Canty G. A. (1993). Impact significance determination - Basic considerations and sequenced approach. Environ Impact Assess Rev. 13 (5), 275-297. DOI.10.1016/0195-9255(93)90020-C.

Cardenas, I.C., Halman, J.I.M. (2016). Coping with uncertainty in environmental impact assessments: Open techniques. Environmental Impact Assessment Review. (60), 24–39. DOI.10.1016/j.eiar.2016.02.006.

Cashmore, M., Richardson, T., Hilding-Ryedvik, T., Emmelin, L. (2010). Evaluating the effectiveness of impact assessment instruments: Theorising the nature and implications of their political constitution. Environmental Impact Assessment Review. 30 (6), 371–379. DOI.10.1016/j.eiar.2010.01.004.

Cloquell-Ballester, V.A., Monteverde Días, R., Cloquell-Ballester, V.A., Santamarina-Siurana, M.C. (2007). Systematic comparative and sensitivity analyses of additive and outranking techniques for supporting impact significance assessments. Environmental Impact Assessment Review. 27 (1), 62–83. DOI.10.1016/j.eiar.2006.08.005.

Conesa Fdez.-Vítora, Vicente. (1997). Guía Metodológica para la Elaboración de una Evaluación de Impacto Ambiental. 3ª edición. MundiPrensa. Madrid. 284 pp.

Conesa Fdez.-Vítora, Vicente. (2010). Guía Metodológica para la Elaboración de una Evaluación de Impacto Ambiental. 4a edición revisada y ampliada. MundiPrensa. Madrid. 864 pp.

Couso, I., Sánchez, L. (2010). Inner and outer fuzzy approximations of confidence intervals. Fuzzy Sets and Systems. 184 (1-1). 68-83. DOI.10.1016/j.fss.2010.11.004.

Dubois, D., Prade, H. (1980). Fuzzy Sets and Systems: Theory and Applications. Mathematics in Science and Engineering. Volume 144. Academic Press. New York. 393 p. DOI.10.2307/2273604.

Dubois, D., Prade, H. (1987). The Mean Value of a Fuzzy Number. Fuzzy Sets and Systems. 24 (3), 279-300. DOI.10.1016/0165-0114(87)90028-5.

Dubois, D., Ostasiewicz, W., Prade. H. (2000). Fuzzy Sets: History and Basic Notions. In: Dubois D., Prade H. (eds). 2000. Fundamentals of Fuzzy Sets. The Handbooks of Fuzzy Sets Series, vol 7. Springer, Boston, MA. DOI.10.1007/978-1-4615-4429-6_2.

Dubois, D., Foulloy, L., Mauris, G., Prade, H. (2004). Probability-Possibility Transformations, Triangular Fuzzy Sets, and Probabilistic Inequalities. Reliable Computing. 10 (4), 273–297. DOI.10.1023/B:REOM.0000032115.22510.b5.

Dubois, D. (2011). The role of fuzzy sets in decision sciences: old techniques and new directions. Fuzzy Sets and Systems. 184 (1).3-28. DOI.10.1016/j.fss.2011.06.003.

Enea, M., Salemi, G. (2001). Fuzzy approach to the environmental impact evaluation. Ecological Modelling 136. 131–147. DOI.org/10.1016/S0304-3800(00)00380-X.

Frini, A., BenAmor, S. (2019). MUPOM: A multi-criteria multi-period outranking method for decision-making in sustainable development context. Environmental Impact Assessment Review 76. 10–25. DOI.org/10.1016/j.eiar.2018.11.002.

Garmendía, A., Salvador, A., Crespo, C., Garmendía, L. (2005). Evaluación de Impacto Ambiental. Pearson Educación S.A. Madrid. 416 pp.

Gómez Orea, Domingo. (2010). Evaluación de Impacto Ambiental. Un instrumento preventivo para la gestión ambiental. 2ª edición. Reimpresión. MundiPrensa. Madrid. 749 pp.

Goyal, S.K., Deshpande, V.A. (2001). Comparison of weight assignment procedures in evaluation of environmental impacts. Environmental Impact Assessment Review. 21 (6), 553-563. DOI.10.1016/S0195-9255(01)00086-5.

Grzegorzewski, P. I., (2002). Nearest interval approximation of a fuzzy number. Fuzzy Sets and Systems, 130 (3), 321 – 330, DOI.0.1016/S0165-0114(02)00098-2.

Hoyos, D. (2010). The state of the art of environmental valuation with discrete choice experiments. Ecological Economics. 69 (8), 1595–1603. DOI.10.1016/j.ecolecon.2010.04.011.

Huang, I. B., Keisler, J., Linkov, I. (2011). Review. Multi-criteria decision analysis in environmental sciences: Ten years of applications and trends. Science of the Total Environment. 409, (19), 3578–3594. DOI.10.1016/j.scitotenv.2011.06.022.

Janssen, R. (2001). On the Use of Multi-Criteria Analysis in Environmental Impact Assessment in The Netherlands. J. Multi-Crit. Decis. Anal. 10, (2), 101–109. DOI: 10.1002/mcda.293.

Jay, S., Jones, C., Slinn, P. Wood, C. (2007). Environmental impact assessment: Retrospect and prospect. Environmental Impact Assessment Review 27. 287–300. DOI.10.1016/j.eiar.2006.12.001.

Ji, C., Hong, T. (2016). New Internet search volume-based weighting method for integrating various environmental impacts. Environmental Impact Assessment Review 56. 128–138. DOI.org/10.1016/j.eiar.2015.09.008.

Juang, C.H., Jhi, Y.Y., Lee, D.H. (1998). Stability analysis of existing slopes considering uncertainty. Engineering Geology 49. 111-122. DOI.org/10.1016/S0013-7952(97)00078-1.

Kågström, M. (2016). Between ‘best’ and ‘good enough’: How consultants guide quality in environmental assessment. Environmental Impact Assessment Review 60. 169–175. DOI.org/10.1016/j.eiar.2016.05.003.

Kamijo, Tetsuya, Huang, Guangwei. (2017). Enhancing the discussion of alternatives in EIA using principle component analysis leads to improved public involvement. Environmental Impact Assessment Review 65. 63–74. DOI.org/10.1016/j.eiar.2017.04.009.

Kang, H., Lee, Y., Kim, S. (2016). Sustainable building assessment tool for project decision makers and its development process. Environmental Impact Assessment Review 58. 34–47. DOI.org/10.1016/j.eiar.2016.02.003.

Kaufmann A., Gupta M.M. (1985). Introduction to fuzzy arithmetic. Theory and application. 1° ed. New York. Van Nostrand Reinhold. 351 pp.

Klir, G.J., Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic. Theory and Applications. Prentice Hall PTR. ISBN 0-13-101171-5. pp. 591.

Kolhoff, A. J., Driessen, P. P. J., Runhaar, H.A.C. (2018). Overcoming low EIA performance - A diagnostic tool for the deliberate development of EIA system capacities in low and middle income countries. Environmental Impact Assessment Review 68. 98–108. DOI.org/10.1016/j.eiar.2017.11.001.

Landeta, Jon. (1999). El Método Delphi. Una Técnica de Previsión del Futuro. Ariel. Barcelona. 223 pp.

Leopold, L., Clarke, F., Hanshaw, B. y Balsley, J. (1971). A Procedure for Evaluating Environmental Impact. U. S. Geological Survey Circular 645. United States Department of the Interior. Washington. DOI:10.3133/circ645.

Leung, W., Noble, B., Gunn. J., Jaeger, J. A. G. (2015). A review of uncertainty research in impact assessment. Environmental Impact Assessment Review 50. 116–123. DOI.org/10.1016/j.eiar.2014.09.005.

Li, L., Fan, G. (2014). Fuzzy MADM with Triangular Numbers for Project Investment Model based on Left and Right Scores. Research Journal of Applied Sciences, Engineering and Technology. 7 (13), 2793-2797. DOI.10.19026/rjaset.7.601.

Lin, Y., Cheng, H-P., Tseng, M-L., Tsai, J. C. C. (2010). Using QFD and ANP to analyze the environmental production requirements in linguistic preferences. Expert Systems with Applications. 37 (3), 2186–2196. DOI.10.1016/j.eswa.2009.07.065.

Llamas, S., Barón, J. (2019). Procedimiento Metodológico para la Ponderación Relativa de la Importancia Ambiental de las Acciones de Proyectos. Revista Tecnología y Ciencia. 36. 51-70. DOI.org/10.33414/rtyc.36.51-70.2019.

Loomis, J. J., Dziedzicb, M. (2018). Evaluating EIA systems effectiveness: A state of the art. Environmental Impact Assessment Review 68. 29–37. DOI.org/10.1016/j.eiar.2017.10.005.

Morgan, R. K. (2012). Environmental impact assessment: the state of the art. Impact Assessment and Project Appraisal. 30 (1), 5–14. DOI.10.1080/14615517.2012.661557.

Morgan, R. K. (2017). Conceptualizing best practice in impact assessment. Environmental Impact Assessment Review 66. 78–85. DOI.10.1016/j.eiar.2017.06.009.

NG, C. Y. (2016). An evidential reasoning-based AHP approach for the selection of environmentally-friendly designs. Environmental Impact Assessment Review 61. 1–7. DOI.org/10.1016/j.eiar.2016.06.006.

Parashar, A., Paliwal, R., Rambabu, P. (1997). Utility of fuzzy cross-impact simulation in Environmental Assessment. Environ Impact Assess. Rev. 17.427-447. DOI.org/10.1016/S0195-9255(97)00046-2.

Peche, R., Rodríguez, E. (2009). Environmental impact assessment procedure: A new approach based on fuzzy logic. Environmental Impact Assessment Review. 29 (5), 275-283. DOI.10.1016/j.eiar.2009.01.005.

Pölönen, I., Hokkanen, P. Jalava, K. (2011). The effectiveness of the Finnish EIA system - What works, what doesn't, and what could be improved? Environmental Impact Assessment Review. 31 (2), 120–128, DOI.10.1016/j.eiar.2010.06.003.

Rahimi, E., Ghasemzadeh, H. (2015). A new algorithm to determine optimum cut-off grades considering technical, economical, environmental and social aspects. Resources Policy 46. 51–63. DOI.org/10.1016/j.resourpol.2015.06.004.

Ramanathan, R. (2001). A note on the use of the analytic hierarchy process for environmental impact assessment. Journal of Environmental Management. 63, (1), 27–35. DOI.10.1006/jema.2001.0455.

Rathi, A. K. A. (2017). Evaluation of project-level environmental impact assessment and SWOT analysis of EIA process in India. Environmental Impact Assessment Review 67. 31–39. DOI.org/10.1016/j.eiar.2017.08.004.

Reguant-Álvarez, M., Torrado-Fonseca, M. (2016). El método Delphi. REIRE, Vol. 9, núm. 1. ISSN:2013-2255. DOI:10.1344/reire2016.9.1916.

Saaty, T. L. (1977). A scaling method for priorities in hierarchical structures. Journal of Mathematical Psychology. 15 (3), 234-281. DOI.10.1016/0022-2496(77)90033-5.

Saaty, T.L. (1978). Modeling Unstructured Decision Problems - The Theory of Analytical Hierarchies. Mathematics and Computers in Simulation. 20 (3), 147-158. DOI.10.1016/0378-4754(78)90064-2.

Saaty, R. W. (1987). The Analytic Hierarchy Process-What it is and how it to used. Mathematical Modelling. 9. (3-5), 161-176. DOI.10.1016/0270-0255(87)90473-8.

Saaty, T. L. (2008). Decision making with the analytic hierarchy process. Int. J. Services Sciences. 1 (1), 83-98. DOI.10.1504/IJSSCI.2008.017590.

Steinemann, A. (2001). Improving alternatives for environmental impact assessment. Environmental Impact Assessment Review. 21 (1), 3-21. DOI.10.1016/S0195-9255(00)00075-5.

Stewart, T. J. Janssen, R. (2013). Integrated Value Function Construction with Application to Impact Assessments. International Transactions in Operational Research 20. 559-578. DOI.org/10.1111/itor.12016.

Swor, T., Canter, L. (2011). Promoting environmental sustainability via an expert elicitation process. Environmental Impact Assessment Review. 2011. 31 (15), 506–514. DOI.10.1016/j.eiar.2011.01.014.

Thompson, M. A. (1990). Determining impact significance in EIA: a review of 24 methodologies. Journal of Environmental Management. 30 (3), 235-250. DOI.10.1016/0301-4797(90)90004-G.

Toro, J., Requena, I., Duarte, O., Zamorano, M. (2013). A qualitative method proposal to improve environmental impact assessment. Environmental Impact Assessment Review. 43, 9–20. DOI.10.1016/j.eiar.2013.04.004.

Tran, L.T., O´neil, R.V., Smith, E.R. (2009). Determine the most influencing stressors and the most susceptible resources for environmental integrated assessment. Ecological Modelling. 220 (18), 2335-2340. DOI.10.1016/j.ecolmodel.2009.06.013.

Villarreal Larrinaga, O., Landeta Rodríguez, J. El Estudio de Casos como Metodología de Investigación Científica en Dirección y Economía de la Empresa. Una Aplicación a la Internacionalización. Investigaciones Europeas de Dirección y Economía de la Empresa [en línea]. 2010, 16(3), 31-52. [fecha de Consulta 8 de Mayo de 2020]. ISSN: 1135-2523. Disponible en: https://www.redalyc.org/articulo.oa?id=274119490001.

Zadeh, L. A. (1965). Fuzzy Sets. Information and Control. 8 (3), 338-353. DOI.10.1016/S0019-9958(65)90241-X.

Zadeh, L. A. (1971). Quantitative Fuzzy Semantics. Information Sciences. 3 (2), 159-176. DOI.10.1016/S0020-0255(71)80004-X.

Zadeh, L. A. (1978). Fuzzy Sets as a Basis for the Theory of Possibility. Fuzzy Sets and Systems. 1 (1), 3-28. DOI.10.1016/0165-0114(78)90029-5.

Zadeh, L. A. (1999). Fuzzy Sets as a Basis for a Theory of Possibility. Fuzzy Sets and System. (100), 1, 9-34, DOI.10.1016/S0165-0114(99)80004-9.

Zhang, J., Kørnøv, L., Christensen, P. (2013). Critical factors for EIA implementation: Literature review and research options. Journal of Environmental Management 114. 148-157, DOI.10.1016/j.jenvman.2012.10.030.

Zhao, M. Y., Cheng, C. T., Chau, K. W., Li, G. (2006). Multiple criteria data envelopment analysis for full ranking units associated to environment impact assessment. International Journal of Environment and Pollution. 28 (3-4), 448-464. DOI.10.1504/IJEP.2006.011222.