>
Revista Tecnología y Ciencia - Universidad Tecnológica Nacional
DOI:https://doi.org/10.33414/rtyc.35.123-136.2019 - ISSN 1666-693 -
Junio 2019 / Año 17 - Nº 35
Actas de las IX Jornadas Argentinas de Robótica 15-17 de noviembre, Córdoba, Argentina
Plataforma de Emulación de Animales Cuadrúpedos: Cinemática de las Patas
Quadruped Animal Emulation Platform: Kinematics of the Legs
Presentación: 17/11/2017
Aprobación: 02/12/2017
Hugo N. Pailos
Laboratorio de Animatrónica y Control Dinámico, Facultad de Ciencias Exactas, Físicas y Naturales, Universidad Nacional de Córdoba. Córdoba - Argentina.
hpailos@gmail.com
Guillermo Bima
Laboratorio de Animatrónica y Control Dinámico, Facultad de Ciencias Exactas, Físicas y Naturales, Universidad Nacional de Córdoba. Córdoba - Argentina.
guillermobima@hotmail.com
Ariel Libal
Laboratorio de Animatrónica y Control Dinámico, Facultad de Ciencias Exactas, Físicas y Naturales, Universidad Nacional de Córdoba. Córdoba - Argentina.
ariel_libal@hotmail.com
Resumen
En este trabajo se presenta un robot de cuatro patas que posee dos servomotores por pata (ocho en total), localizados en los hombros y codos en los cuartos delanteros y en las caderas y rodillas en los cuartos traseros. El diseño, construcción y programación de este robot, tiene como objetivo la emulación de animales cuadrúpedos. Esta plataforma robot, puede caminar de diferentes maneras para imitar tanto animales existentes como así también cuadrúpedos extintos. El robot puede caminar hacia delante y hacia atrás y además hacerlo con diferentes estrategias sin caerse.
Palabras claves: Plataforma, Robotizada Cinemática, Cuadrúpedos, Animatrónica
Abstract
This paper presents a four-legged robot that has two servomotors per leg (eight in total), located on the shoulders and elbows in the forequarters and on the hips and knees in the hindquarters. The design, construction and programming of this robot, aims to emulate quadruped animals. This robot platform, can walk in different ways to imitate both existing animals as well as extinct quadrupeds. The robot can walk forward and backward and also do it with different strategies without falling.
keywords:Platform, Robotized Kinematics, Quadrupeds, Animatronics
INTRODUCCIÓN
Desde el punto de vista de la investigación básica el interés de la construcción de robots caminantes en lugar de robots móviles tipo vehículos, está dada en una primera instancia, en la capacidad de los robots con patas para esquivar o sortear obstáculos en un espacio determinado como puede ser el terreno natural [11]. La intención de este trabajo es estudiar la cinemática de las piernas de una plataforma para luego, en posteriores trapajos investigar la dinámica y estabilidad de la misma [12]. Motiva el estudio la construcción de robots y animatrónicos que emulan seres extintos para su posterior exhibición, el trabajo tiene por objetivo principal el estudio, desarrollo y construcción de una plataforma robótica cuadrúpeda básica cuyos cinemática [4] pueda ser predicha mediante el método de Denavit-Hartenberg y plasmar en mismo en un procesador para que éste pueda mover las patas de la plataforma, pensando en mejorar el sistema completo en futuros proyectos [13].
DESCRIPCIÓN DE LA PLATAFORMA
La plataforma diseñada y construida, consta de una base plana y cuatro patas. Cada pata posee dos articulaciones, hombro-codo para las delanteras y cadera-rodilla para los cuartos traseros. Las articulaciones son accionadas por servomotores, ubicados de tal forma que proporcionen la mayor amplitud posible de movimiento. La plataforma esquematiza la morfología de un mamífero cuadrúpedo en forma genérica y simplificada; las configuraciones de las patas son:
Patas delanteras codos hacia atrás.
Patas traseras rodillas hacia delante, como se puede ver el dibujo Fi g.1
Fig. 1: Configuración de las patas de la plataforma.
Si bien esta configuración no es del todo eficiente desde el punto de vista robótico, el lector debe saber que los animatrónicos son robots que emulan personajes, animales actuales y extintos de modo que la configuración elegida tiene como objetivo primordial emular un mamífero, de allí su postura inicial.
CINEMÁTICA DE LA PLATAFORMA
El problema cinemático se divide en dos fases: [2] la cinemática directa y la cinemática inversa. Para el caso en estudio se abordará la cinemática directa mediante la convención de Denavit—Hartenberg (D_H) y para la cinemática inversa se solucionará mediante el teorema del coseno. Recordando que la cinemática directa permite averiguar la posición y orientación del efector final ingresando los ángulos de las articulaciones y que la Cinemática inversa permite saber los ángulos de las articulaciones dados una posición y orientación; es que mostramos un esquema para mayor entendimiento en la fig. 2
Fig. 2: El Problema Cinemático.
A. Cinemática Di recta
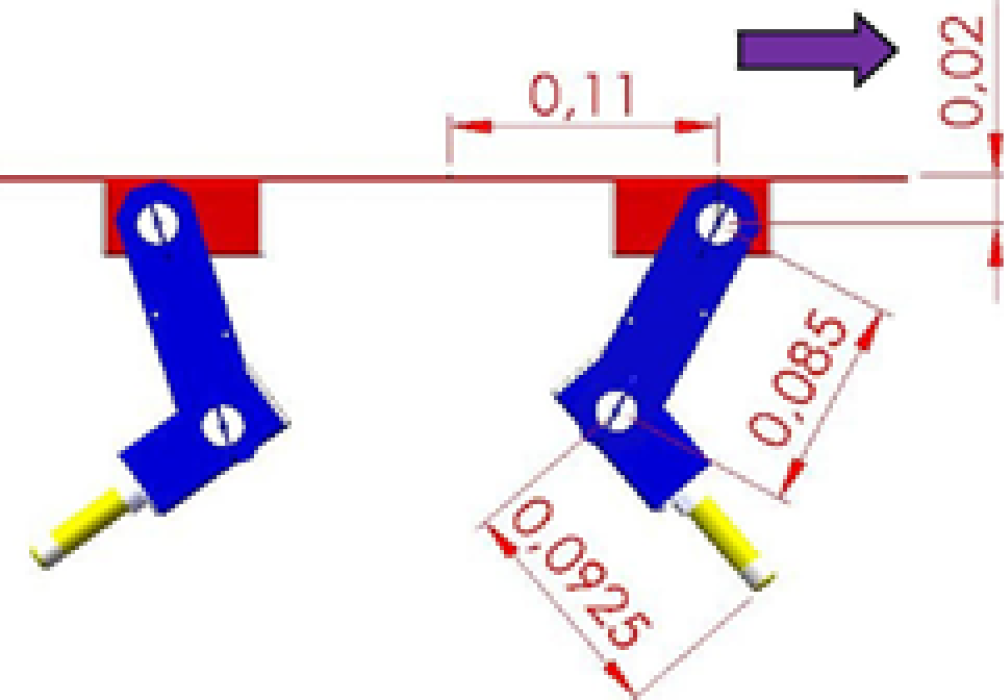
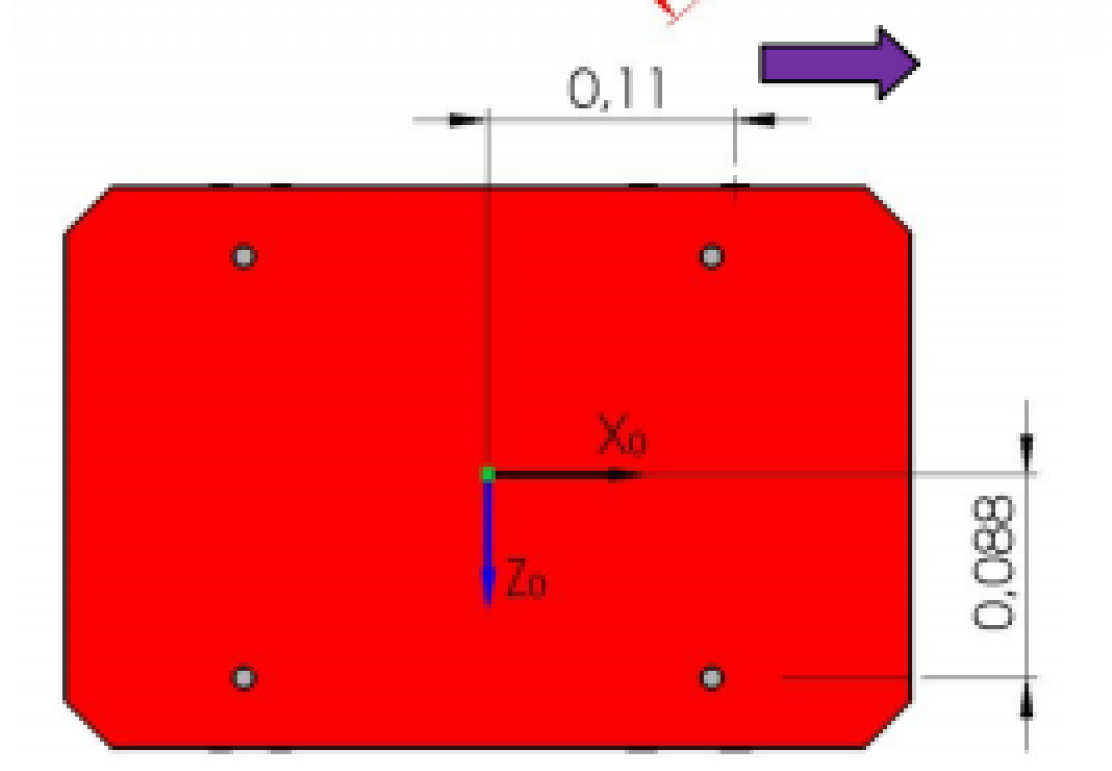
Para identificar los parámetros (D_H) es necesario tener en cuenta las dimensiones de la plataforma con las medidas relevantes, en la fig. 3 se pueden ver las dimensiones.
Fig. 3: Dimensiones de la plataforma en metros.
Para tener la posibilidad de controlar la posición y velocidad de cada articulación, se utilizaron servomotores, se adoptaron servomotores del tipo conocido como RC (por su uso en radio control) de 0.012 kg./m. de torque.
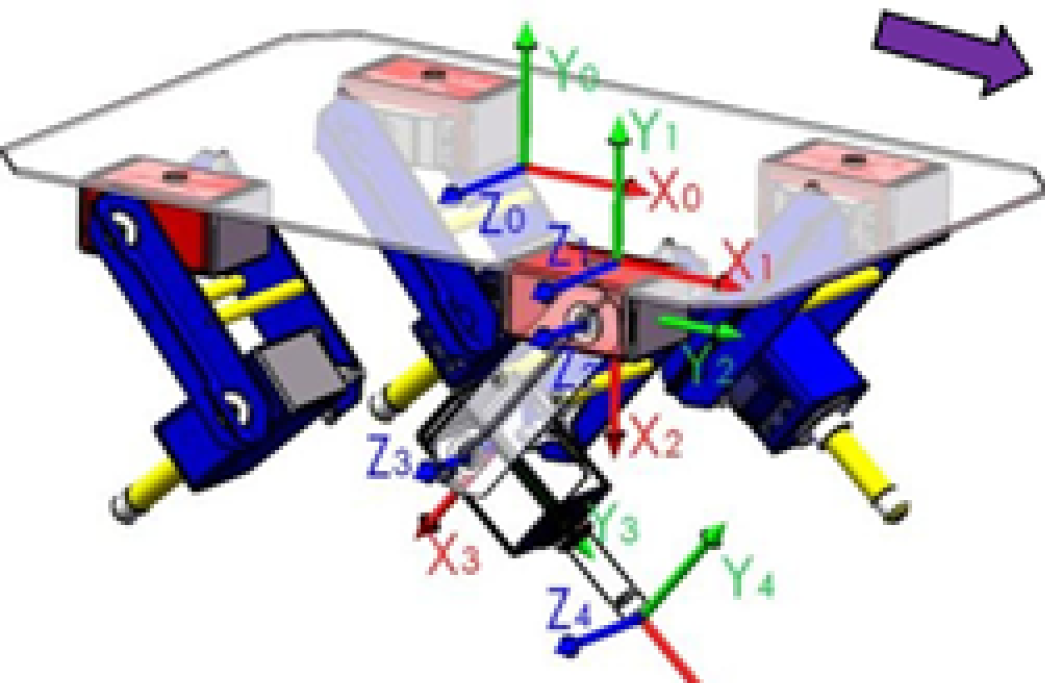
Fig. 4: Ejes de acuerdo al algoritmo de (D_H).
Lo primero que se hizo para obtener estos parámetros de acuerdo a [3] es ubicar los ejes (x,y,z) desde el centro de la plataforma (x,,yo,zo) hasta el efector final que es la planta del pie del robot (x4,y4,z4); de acuerdo al procedimiento se obtienen los siguientes sistemas:
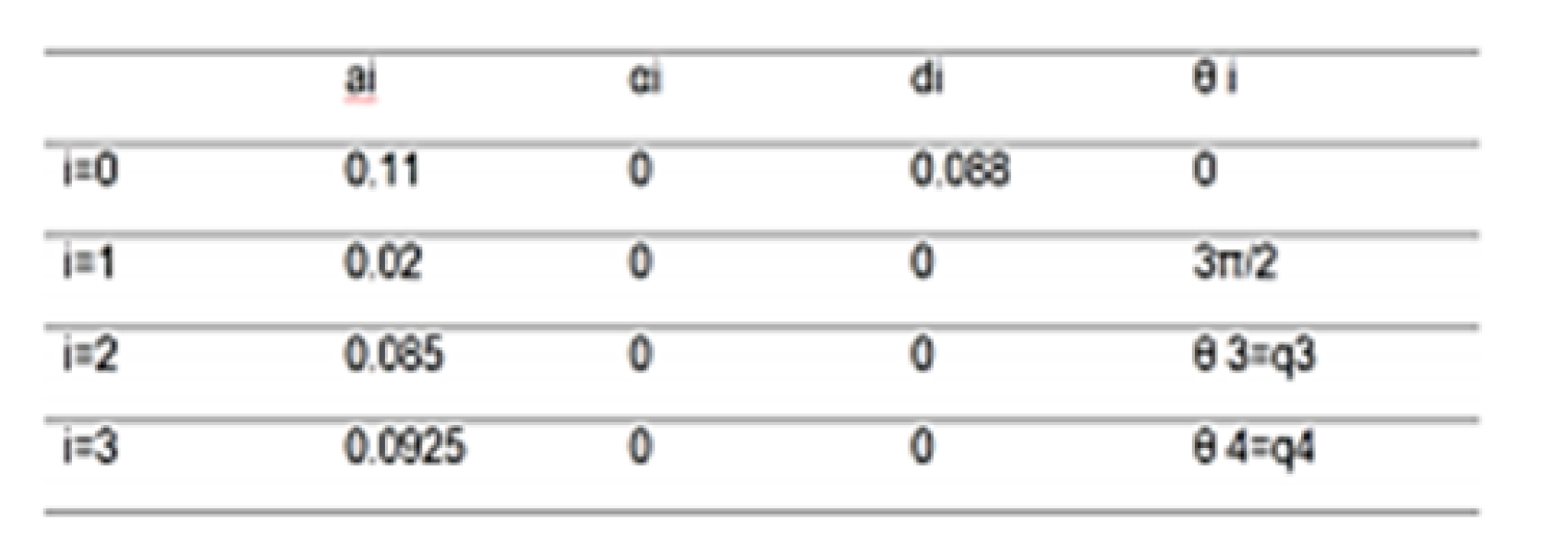
Recordando que parámetros (D_H) permiten definir completamente el algoritmo para obtener la cinemática directa, según[4]. y que se trata de cuatro conjuntos de datos a saber: q3 y q4 son los ángulos correspondientes a los servos de hombro y codo en las patas delanteras y de cadera y rodilla en la patas traseras, el resto corresponde a distancias propias de la plataforma y a ángulos en los que se definen los sistemas posicional es relativos en cada articulación. Se listan a continuación en la Tabla 1 los parámetros de (D_H) calculados desde el centro de la plataforma (Xo,Yo Zo) para la pata delantera derecha.
Tabla 1. Parámetros de Denavit Hartenberq - Medidas en metros
Cabe destacar que se deben obtener los parámetros de (D_H) para las cuatro patas para resolver la caminata del robot; la siguiente matriz corresponde a la pata delantera derecha Recordemos que "e" representa el coseno y "s" representa el seno.
Las matrices que referencian el sistema 4 al 3 y el sistema 3 al 2 son
Las matrices que referencian el sistema 2 al 1 y el sistema 1 al O son
Para lograr obtener la matriz completa solo tendremos que multiplica (1) y (2) en el orden expresado
Si analizamos el resultado del producto total es:
En donde los nueve primeros elementos representan la orientación: (n, s y a) y la última columna representa la posición del efector final (en este caso la planta del pie). O sea, que si damos valores a los ángulos q3 y q4, que son los que corresponden a las articulaciones de hombro y codo podríamos saber la posición y orientación de la planta del pie. Hemos calculado la Cinemática directa de la pata derecha del robot y podríamos calcular la de las otras tres patas de forma similar.
B. Cinemática Inversa
Recordemos que este problema puede tener múltiples soluciones. Para el caso de la plataforma lo que se necesita es describir una curva con el efector final que es la planta del pie del robot en el espacio de trabajo y saber que sucesión de ángulos de q3 y q4 se debe programa para describir dicha curva, de modo que el robot camina. Sin embargo el problema principal es, primero: dada una posición (y orientación) en el espacio de trabajo, calcular cuales son los q3 y q4 que colocando esos valores dan una posición determinada. Por lo tanto habrá que buscar un algoritmo que exprese los ángulos q3 y q4 en función de la posición determinada (cinemática Inversa). En la Fig. 5 se expresan los ángulos q3 y q4 para la identificación de los mismos cuando se los utilice en el primer cuadrante para el algoritmo de la cinemática inversa

Discusión acerca de la orientación. En realidad lo que debe ingresar al algoritmo de la cinemática inversa son la posición y la orientación, pero como la pata del robot, tiene solo dos grados de libertad y por ello pocas posibilidades de orientación, buscamos un algoritmo en el que se ingresa sólo posición, y con esa posición develar q3 y q4. Si bien teóricamente las soluciones en determinados puntos del área de trabajo pueden ser dobles; esto es para las patas del alteras codo adelante o codo atrás y a su vez para las patas traseras rodilla adelante o rodilla atrás, solo se está interesado en:
Patas delanteras: codo hacia atrás.
Patas traseras: rodilla adelanta
Puesto que esa es la posición en los mamíferos que representa este robot. En la fig. 6 podemos ver una asignación de ejes para las patas del robot. Si bien está claro que por las "constrains" o restricciones mecánicas de la plataforma las patas solo se podrán mover en el tercero y cuarto cuadrante (pues si se movieran en el primero y segundo, atravesarían la plataforma), calcularemos la cinemática inversa para el primer cuadrante y la comprobaremos para todos los cuadrantes.
Fig. 6: Cuadrantes a partir de la primera articulación.
Llamando: p(1) = coordenada en x; p(2) = coordenada en y; p(3) = coordenada el z, (en este caso es cero porque estamos trabajando en el plano x y).

Esta expresión (6) nos permite calcular q4 en función de las coordenadas p(1) y p(2) pero por motivos computacionales es más conveniente utilizar la expresión de la cotangente según [5]. Entonces necesitamos calcular el senq3
Como se observa en la ecuación (8) existen dos posibles soluciones para q4 según se tome el signo positivo o negativo de la raíz, éstas corresponden a las configuraciones con los nombres de codo arriba y codo abajo en el vocabulario de robótica Sin embargo como expresamos anteriormente, éstas configuraciones son importantes para el análisis de las soluciones; pero inconsistentes con nuestra plataforma, porque atravesarían la misma; solo interesan las soluciones en el tercer y cuarto cuadrante que es el área donde trabajan las patas en la caminata real donde se van a generar las trayectorias para que el robot camine. En este punto se solucionan tanto la cinemática directa como la inversa del robot.
GENERACIÓN DE TRAYECTORIAS
La generación de trayectoria depende del tipo de caminata o estrategia de caminata esto es: ¿Qué patas asientan el piso y cuales están en el aire?, si bien el robot puede hacer varios tipos de caminata se toma una común para ver la trayectoria. Para ello se define:
PDI : pata delantera izquierda
PTI : pata trasera izquierda .
PTD: Pata trasera derecha.
PDD : pata delantera derecha
avance: pata traccionando en el suelo. retracción: pata volviendo en el aire.

Fig. 8: Secuencia de movimiento de las cuatro patas del robot para que camine.
Es claro que el procesador deberá mover las cuatro patas (ocho servos) al mismo tiempo avanzando dos de ellas y retrayendo (reposicionando) las otras dos. Cada movimiento en cada pata implica dos movimientos en la misma que se traducen en dos curvas del final de cada eslabón: La curva correspondiente al codo y la correspondiente a la mano en las patas delanteras y las curvas correspondientes a las rodillas y las plantas del pie en las patas traseras. Ambas curvas en cada pata son debidas a sus correspondientes servos que están alojados en las patas delanteras en el hombro y codo, y en las traseras en cadera y rodilla. Recordando que los ángulos que producen los movimientos hombro y caderas son llamados q3, y los correspondientes a los codos y las rodillas son llamados q4, es que deberemos generar un conjunto de ángulos sucesivos para cada articulación de cada pata para producir un movimiento continuo de avance [7] a las curvas que realizan las plantas se las llaman trayectorias, y al firmware o software que las realiza, "generador de trayectorias". En la fig. 9 se muestra un dispositivo "manual" utilizando solo transportadores y reglas comunes para hacer generaciones de trayectoria de ambas patas (delanteras y traseras) al mismo tiempo, esto es porque las dimensiones de la plataforma así lo permiten.
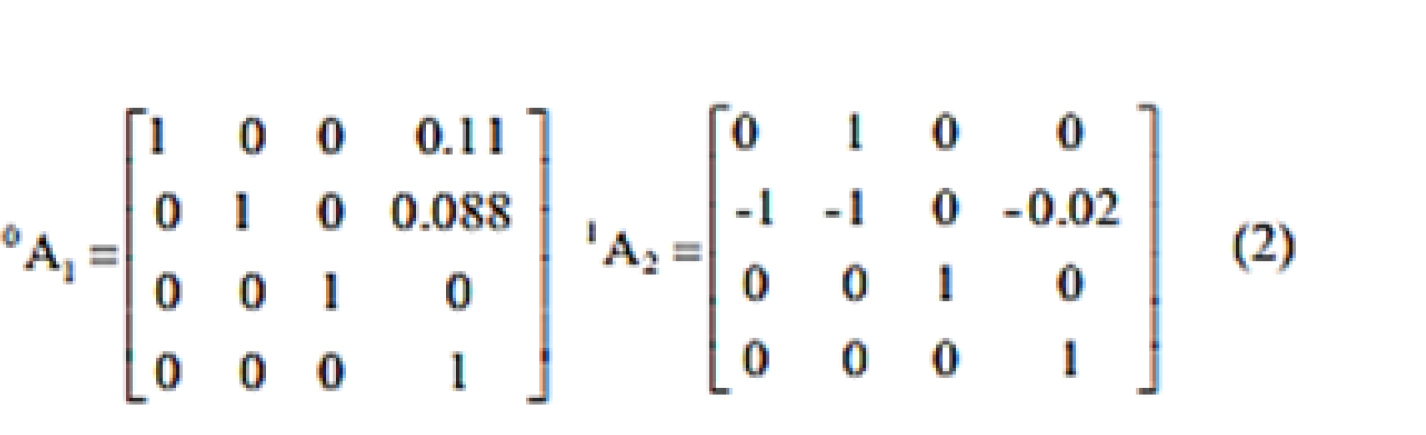
Fig. 9: Dispositivo manual para “dibujar” trayectorias de las patas de la plataforma.
La secuencia es generada con este dispositivo por cuestiones didácticas, pero las trayectorias se toman de un animal vivo, en este caso un perro mediante el uso del video [7]
Obsérvese que si se mueve el extremo del dispositivo, se pueden "dibujar" trayectorias de ambas patas (traseras y delanteras); la rodilla hacia delante, representa a una pata trasera de los lados derecho e izquierdo de la plataforma y el codo hacia atrás representan las patas delanteras de ambos lados de la plataforma; sin embrago y para lograr una mayor precisión en la secuencia de los ángulos, se utilizó Autocad y Matlab [5] para la secuencia de ángulos q3 y q4.
En la siguiente Tabla 2 se muestran la secuencia que deben seguir los servomotores para conseguir una caminata estable; lo puntos suspensivos representan el resto de los valores de los ángulos.

Tabla 2. Secuencia de ángulos de cada servo de cada pata para lograr una caminata estable.
Esta secuencia generada en los servos en la pata delantera derecha da como resultado las posiciones que se muestran en la f i gura 10.
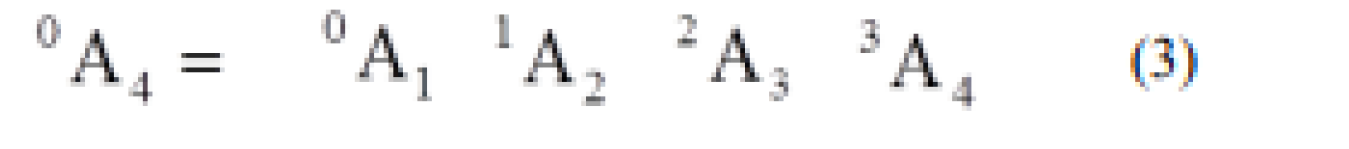
Fig. 10 Secuencia de posiciones de una pata delantera derecha
Si ahora observamos nuevamente la Fig. 8 en la que se muestran las acciones de tracción y retracción que el procesador deberá generar en cada paso es simple deducir que siguiendo los cuatro tiempos expresados en la Fi g.8 correspondientes a las cuatro patas del robot, se logra una caminata estable que luego se comprueba en la práctica con las cuatro patas desfasadas en el tiempo exactamente a un cuarto de tiempo que dura el ciclo completo de una pata en el que demora en la acción de tracción y retracción conjuntas de acuerdo al video base del estudio [7]
PROCESADOR Y CONTROL DE LA PLATAFORMA
El procesador es una placa Arduino® Mega 2560 Basado en un microcontrolador ATmega2560. [1] Este chip trabaja a 16Mhz y con un voltaje de 5v. Esta tarjeta de 8 bits trabaja conjuntamente con una SRAM de 8KB, 4KB de EEPROM y 256KB de flash (8KB para el bootloader) [1].
En cuanto a características electrónicas, el número de pines es 54 pines digitales (15 de ellos PWM) y 16 pines analógicos. El control del robot se realiza por medio de esta placa que determina la posición de cada uno de los ocho servos en todo momento respetando la Tabla 2 para la pata delantera derecha; las otras tres tablas que no se expresan por razones de espacio en este trabajo. El micro maneja perfectamente la secuencia de cada servo. Se programa con todos los datos obtenidos de cada pata por el método de Denavit Hartemberg adaptando los valores del método a los valores reales de los servos (mapear) puesto que los servos están colocados en forma simétrica en la plataforma de modo que si bien en (D_H) da una secuencia de ángulos progresiva hacia arriba, en el servo la secuencia puede ser al revés por estar colocado físicamente en forma opuesta a los sistemas que se usan en (D_H); el procesador elegido permite hacer esta adaptación de manera simple [6].
Se tuvo que hacer además pruebas de offset para que el procesador "tomara como arranque" de la trayectoria los valores específicos que distan en todos los casos de "un cero" de servo.
CONCLUSIONES.
El diseño, la construcción y la programación de la plataforma responden en forma que el robot puede marchar sin caerse, logrando que la plataforma pueda caminar en forma estable emulando diferentes animales cuadrúpedos. Si bien en el presente trabajo solo se emula la caminata de un perro [7], el robot puede emular diferentes animales actuales y extintos. Se estudió el robot completo desde un enfoque clásico y particularmente empleando la parametrización de Denavit - Hatenberg para realizar la modelización y el estudio del problema y se comprueba tanto teórica como prácticamente que dicho algoritmo puede ayudar a la sistematización de problemas de robots caminantes, esto es ayudar a modelarlos matemáticamente y en una etapa posterior a resolver problemas de estabilidad en otras estrategias de marcha en robot cuadrúpedos. Se desarrolló tanto la cinemática directa como la inversa de las patas del robot y ambas fueron simuladas, programadas, y verificadas por medio del software Matlád y empíricamente, dando resultados que luego se implementaron en el procesador elegido para lograr la secuencia adecuada para que el robot camine. Se construyó el robot y camina hacia delante y hacia atrás sin caerse.
REFERENCIAS
[1] Artero Oscar Torrente (2014). "Arduino, Curso práctico de formación". Alfaomega. Colombia
[2] Barrientos, E. A., "Fundamentos de Robótica". Mcgraw-Hill / Interamericana De España. España (1997).
[3] Xuewen Rong1, Yibin Li 1, Juhong Ruan2 and Hongjun Song "Kinematics Analysis and S mulati on of a Quadruped Robot" School of Control Science and Engineering, Shandong University, China advanced Vehicle and Robot Institute, Shandong Jaotong University, China Applied Mechanics and Materials Vola 26-28 (2010) pp 517-522 Online available si nce 2010/Jun/30 at www.scientific.net © (2010) Trans Tech Publications,Switzerland
doi :10.4028/www.scientific.net/AM M.26-28.51
[4] Joaquin Estremera and Kenneth J. Waldron "Leg Thrust Control for Stabilization of Dynamic Gaits in a Quadruped Robot" Stanford University, Department of Mechanical Engineering, Palo Alto, CA, USA. Springer (2006)
.[5] Jonas Buchli, Mrinal Kalakrishnan, Michael Mistry, Peter Pastor, and Stefan Schaal "Compliant Quadruped Locomotion Over Rough Terrain" Computational Learning and Motor Control Lab, University of Southern California Los Angeles (2009)
[6] Spong, M. e. a "Robot Modeling and Control ". si:John Wiley & Sons. (2006).
[7] Stelian Coros, Andrej Karpathy, Ben Jones, Lionel Reveret, Michiel van de Panne (2011) “Locomotion skills for simulated quadrupeds”. (https://www.youtube.com/watch?v=dRthdBr46c)
[8] Behnam Miripour (2010). “Climbing and walking robots”. Open Access. Edited by Behnam Miripour, Publisher: InTech. 2010. http://www.intechopen.com/books/climbing-andwalking-robots.
[9] Annalisa MilellaDonato Di Paola and Grazia Cicirell “Mechatronic systems simulation modeling and control” Edited by i, 306 pages, Publisher: InTech. (2010).
[10] Roland Illah, “Introduction to autonomous mobile robots”. Siegwart Nourbakhsh, (2004).
[11] Yibin Li, Bin Li, Jiuhong Ruan and Xuewen Rong, “Research of Mammal Bionic Quadruped Robots: a Review” Member, IEEE (2011)
[12]Keisuke Arikawa 1 And Shigeo Hirose 2 “Mechanical design of walking machines” 1Department of Mechanical Ingineering, Kanagawa Institute of Technology, 1030 Shimoogino, Atsugi-shi, Kanagawa 243-0292, Japan, 2 Department of Mechanical and Aerospace Engineering, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8550, Japan (2006)
[13] Elena García Armada “Optimización de la estabilidad y la velocidad de robots caminantes” tesis Doctoral Ingeniera Industrial por la ETSII Universidad Politécnica De Madrid Escuela Técnica Superior De Ingenieros Industriales (2002)