Revista Tecnología y Ciencia - Universidad Tecnológica Nacional
Año 20 - Número 45 / Sep - Dic
2022
DOI:https://doi.org/10.33414/rtyc.45.46-66.2022
ISSN 1666-6933
Reconocimiento-NoComercial 4.0 Internacional
Parámetros del dominio de la frecuencia de pulsos de descargas parciales (DP), para la construcción de mapas de clasificación que permitan la separación de fuentes de DP, en mediciones en línea.
Frequency domain Partial Discharge (PD) pulse parameters for the construction of classifications maps that allow the separation of PD sources in online measurements
Presentación: 22/09/2022
Aprobación: 02/12/2022
Damián Verna
Centro de Investigación, Desarrollo e Innovación en Energía Eléctrica, Facultad Regional General Pacheco, Universidad Tecnológica Nacional – Argentina.
damian.verna@alumnos.frgp.utn.edu.ar
Gerardo Kocsis
Centro de Investigación, Desarrollo e Innovación en Energía Eléctrica, Facultad Regional General Pacheco, Universidad Tecnológica Nacional – Argentina.
gkocsis@docentes.frgp.utn.edu.ar
Hector Pocetti
Centro de Investigación, Desarrollo e Innovación en Energía Eléctrica, Facultad Regional General Pacheco, Universidad Tecnológica Nacional – Argentina.
hpocetti@docentes.frgp.utn.edu.ar
Cristian Bonini
Centro de Investigación, Desarrollo e Innovación en Energía Eléctrica, Facultad Regional General Pacheco, Universidad Tecnológica Nacional – Argentina.
cbonini@docentes.frgp.utn.edu.ar
Marcos Maillot
Centro de Investigación, Desarrollo e Innovación en Energía Eléctrica, Facultad Regional General Pacheco, Universidad Tecnológica Nacional – Argentina.
mmaillot@docentes.frgp.utn.edu.ar
RESUMEN
En este trabajo se estudian las características en el dominio de la frecuencia de pulsos de Descargas Parciales (DP), con el objeto de conformar mapas de clasificación que permitan separar distintas fuentes de pulsos. Dichos mapas son aplicados en las mediciones en línea de DP, donde múltiples fuentes están presentes y, mediante éstos, es posible separar las distintas fuentes y graficar su subpatrón correspondiente, para realizar la identificación de la fuente.
Las características que se analizaron en el dominio de las frecuencias fueron: energía (Vef), módulo máximo (Xmax), frecuencia del módulo máximo (fmax) y ancho de banda (BW_3db). Estos parámetros se calcularon sobre la descomposición de cada pulso mediante la Transformada de Onditas Discreta (TOD). El algoritmo fue probado, tanto con señales obtenidas en probetas, como sobre equipos reales. Los resultados demostraron que es factible separar fuentes de DP empleando el parámetro módulo máximo (Xmax) para las bandas de frecuencia correspondiente al detalle 5 (7,8 a 15,6 MHz) y al detalle 4 (16,5 a 31,2 MHz).
Palabras clave: Descarga Parcial, Transformada de Onditas Discretas, Mapa de clasificación, Dominio de la Frecuencia
ABSTRACT
In this work, the frequency domain characteristics of partial discharge (PD) pulses are studied to construct classification maps that allow different sources of pulses to be separated. These maps are applied in online PD measurements, where multiple sources are present and through them, it is possible to separate the different sources and graph their corresponding subpattern to identify the source.
The characteristics that were analyzed in the frequency domain were: energy (Vef), maximum modulus (Xmax), maximum modulus frequency (fmax) and bandwidth (BW_3db). These parameters were calculated on the decomposition of each pulse using the Discrete Wavelet Transform (DWT). The algorithm was tested both with signals obtained from test specimens and on real equipment. The results showed that it is feasible to separate PD sources using the maximum modulus parameter (Xmax) for the frequency bands of detail 5 (7.8 to 15.6 MHz) and detail 4 (16.5 to 31.2 MHz).
Keywords: Partial Discharge, Wavelet transform, Classification map, frequency domain.
INTRODUCCIÓN
Una Descarga Parcial (DP) es un fenómeno de ruptura dieléctrica que se produce en el seno de un material aislante. Su ocurrencia se debe a la presencia de impurezas o de oclusiones internas a niveles micro y macromolecular; también, debido a defectos constructivos, aristas o puntas aguzadas capaces de generar gradientes de potencial locales elevados.
Una DP se caracteriza por ser un pulso de corriente no estacionario de alta frecuencia; en este sentido, las normas vigentes IEC 60034-27-2 (2012), IEEE C37.301 (2009) y IEC 60270 (2002) distinguen 4 rangos de frecuencia para la medición de DP:
- Baja Frecuencia (LF): < 3 MHz
- Alta Frecuencia (HF): 3-30 MHz
- Muy Alta Frecuencia (VHF): 30-300 MHz
- Ultra Alta Frecuencia (UHF): 0,3-3 GHz
El rango más extendido es el LF, alcanzado por la norma IEC 60270 (2002) y referenciado en diversos estándares, como el IEEE C37.301 (2009). En este rango, por medio de un calibrador, se obtiene el valor de carga aparente, el cual es utilizado como medida de aceptación o rechazo para diferentes ensayos. La desventaja de las mediciones en LF es que por debajo de los 3 MHz para mediciones en línea (con el equipo en servicio, sin ser desconectado para llevar a cabo la medición) se producen diversas interferencias debido a las señales de onda portadora de las líneas, debido a la conmutación de motores alimentados por variadores de velocidad y debido a perturbaciones en los sistemas de excitación (IEC 60034-27-2, 2012).
En las frecuencias superiores (HF, VHF y UHF), la señal medida no es directamente proporcional a la carga aparente, por lo cual esta no puede determinarse (IEC 60034-27-2, 2012). Adicionalmente, en el caso de medición de máquinas rotativas en estas bandas de frecuencia, el sistema de medición pierde sensibilidad para las DP cuya ocurrencia tenga lugar en las espiras más lejanas al punto de medición (IEC 60034-27-2, 2012). Sin embargo, la medición de DP en este rango de frecuencias trae consigo la posibilidad de implementar herramientas de procesamiento para separar distintas fuentes de pulsos y emitir un diagnóstico de gran precisión, ya que permite descartar señales de ruido para solo analizar aquellas que se asocien a algún tipo de defecto (CIGRE WG D1.37, 2016). Además, en el rango de HF, se puede emplear como captor un transformador de corriente de núcleo partido el cual permite realizar la medición sin retirar el equipo de servicio; configuración que, en cambio, en LF no obtiene una sensibilidad adecuada (Wu et al., 2015).
El monitoreo y la detección temprana de estos fenómenos es de gran importancia para el mantenimiento predictivo de máquinas y equipos eléctricos de potencia (Cavallini et al., 2003b. 2003c; Salcedo et al., 2001). Es importante detectar precozmente estos eventos dado que, una vez iniciado el proceso de descargas, comienza a deteriorarse el medio aislante, con evolución progresiva y altamente nociva para el material dieléctrico que compone la aislación.
La implementación de la medición de DP en línea presenta un gran desafío debido a las distintas fuentes de ruido presentes en una estación transformadora. Gracias al avance de la tecnología, en la actualidad es posible monitorear ciertos parámetros deducidos de la ocurrencia de dichos eventos. Esto permite no solo corroborar que el fenómeno se encuentra activo sino también determinar, mediante un procesamiento matemático adecuado, cuál es la fuente que lo genera (Jiang et al., 2012; Maillot et al., 2018; Paoletti G. J, y Golubev A., 2001). Sin embargo, esta nueva posibilidad trae consigo el problema de procesar una vasta cantidad de información reunida mediante el monitoreo.
Procesamiento de los pulsos de DP para separación de fuentes
En la actualidad, la posibilidad de contar con placas adquisidoras y procesadores de alta velocidad, permite procesar eventos de DP con diferentes herramientas matemáticas, de manera eficiente y en tiempos breves. Si bien, la ocurrencia de estos eventos es indeseable en todo sistema eléctrico de potencia, no todos presentan el mismo grado de nocividad, por lo tanto, es relevante determinar el tipo de falla o fuente que los genera (interna, corona o superficial), mediante el procesamiento matemático de los pulsos de DP adquiridos.
Al realizar mediciones de DP en subestaciones eléctricas, es común observar patrones mezclados debido a la coexistencia de pulsos de DP provenientes de diferentes fuentes y al ruido eléctrico de fondo. Conforme a (Canallini et al., 2002; Hao, L et al., 2011; Kreuger et al., 1993; Bonini et al. 2015), las estructuras que presentan los pulsos correspondientes a DP de tipo interna, de tipo superficial, de tipo corona y las correspondiente al ruido son todas diferentes. Por esta razón, el procesamiento matemático de los pulsos adquiridos correspondientes a un patrón mezclado toma importancia: permite disociar ese patrón en subpatrones correlacionados con las fallas que los generan.
Lo comentado en el último párrafo puede apreciarse en la Figura 1, donde se presenta un patrón de DP con 2 fuentes mezcladas (patrón rojo sobre la izquierda). Luego, a cada pulso adquirido se lo proyecta en un espacio de características o mapa de clasificación (imagen central) y finalmente, a partir de los grupos de puntos formados, se generan los subpatrones de la medición (subpatrones sobre la derecha). La estructura que cada subpatrón exhibe se correlaciona con la fuente que lo genera (Gulski et al., 1992). El presente trabajo está centrado en el desarrollo de un mapa de clasificación capaz de separar, no solo los eventos de DP mezclados proveniente de diferentes fuentes, sino también el ruido.
Figura 1: Concepto de mapa de clasificación y obtención de subpatrones.
En trabajos previos realizados sobre esta temática (Maillot, 2017; Maillot y Pessana., 2018; Maillot et al., 2019), se demostró que, por medio de la descomposición de los pulsos de DP mediante TOD -Transformada de Onditas Discreta- y el cálculo de la energía de sus vectores de coeficientes, es posible construir un mapa de clasificación que permita, a un sistema experto o a un operario, formar grupos de puntos de DP según su fuente. Con los grupos así formados, es posible obtener subpatrones que permitan identificar tipos de DP, tal y como se ejemplifica en la Figura 1.
En tales trabajos, se empleó la energía de cada vector de coeficientes de análisis de TOD para construir el espacio de características empleando las expresiones (7) y (8) (ver sección resultados) sobre cada pulso de DP registrado. De esta manera, se generó un espacio de características de 5 dimensiones, el cual fue reducido a un mapa de 2 dimensiones, para poder visualizarlo, empleando una red neuronal autoorganizada (Maillot et al. 2019) o la técnica de Principal Component Analysis (PCA) (Maillot y Pessana, 2017). Esto hace que se pierda la intuición de lo que representa cada dimensión de dicho mapa de clasificación, con respecto a la información que arroja la descomposición por TOD. Adicionalmente, dichas técnicas producen proyecciones que son dependientes del conjunto de datos empleados, por lo cual, un nuevo set de datos arrojaría como resultado una combinación distinta de las componentes originales del mismo mapa de clasificación. Por estos motivos, en este trabajo se construyen mapas de clasificación de solamente 2 dimensiones, a fin de no necesitar de aplicar técnicas de reducción de dimensiones que sean dependientes de los datos procesados. En dichos mapas de clasificación, se emplearon parámetros del dominio frecuencial de las señales reconstruidas en cada nivel de descomposición alcanzado con la TOD, como se presentará en la sección resultados.
El trabajo continúa con el marco teórico fundamental de TOD para el seguimiento del artículo. Luego, se presentan, dentro de la sección metodología, los aspectos experimentales que se emplearon para la adquisición de los pulsos de DP y las herramientas utilizadas para su procesamiento. En la sección resultados, se presentan los parámetros a calcular en el dominio frecuencial y sus resultados. Luego, se aplica el mapa de clasificación propuesto sobre una medición de un equipo real. Por último, el trabajo finaliza con las conclusiones encontradas en el trabajo.
MARCO TEÓRICO
Transformada de Onditas Discretas
La TOD puede entenderse como: una expansión en series (similar al análisis de series de Fourier) sobre una base de funciones, pertenecientes a un conjunto de subespacios anidados que conforman un análisis de multiresolución (AMR) (Sirne y D’Attellis, 2004). Dicho conjunto de subespacios se generan mediante traslaciones y escalados de dos funciones (ondita ψ(t) y escala φ(t)) según se muestra en las siguientes ecuaciones (1) y (2):
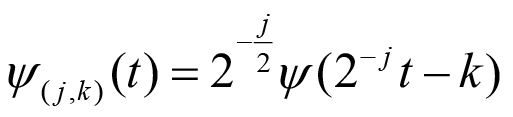 (1)
(1)
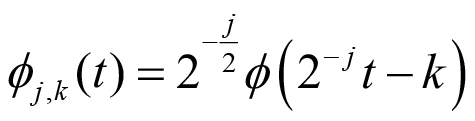 (2)
(2)
En dichas ecuaciones, mediante el parámetro j se construyen las funciones base de los subespacios que conforman el AMR; en donde las funciones onditas ψj (t) definen un subespacio de detalle Wj y las funciones escala φj (t) un subespacio de aproximación Vj. Dadas las ecuaciones [1] y [2] se puede demostrar que cada subespacio de un nivel inferior (j creciente) es contenido por el subespacio inmediato superior de aproximación, como se muestra en la Figura 2, y cumpliéndose lo que señala las ecuaciones (3) a (6):
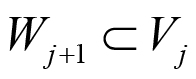 (3)
(3)
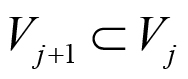 (4)
(4)
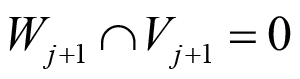 (5)
(5)
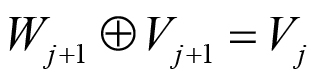
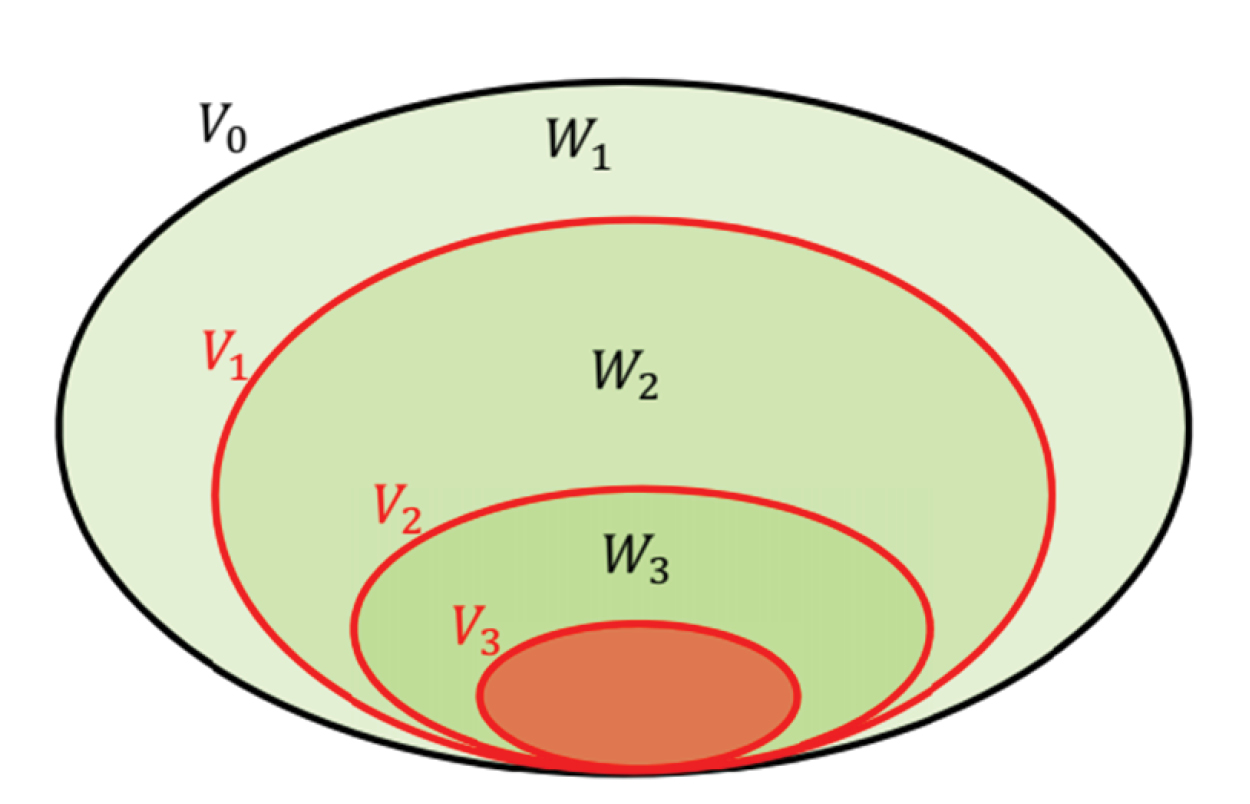
Figura 2: Subespacios anidados de un AMR.
Dada la condición de ortonormalidad que presentan las funciones onditas y escala (Mallat, 2008), la energía de la señal se conserva, lo que permite que esto sea analizado como una descomposición de la energía (o información) del pulso en distintos subespacios.
La implementación de la TOD se puede realizar mediante el algoritmo de banco de filtros (ver Figura 3), el que consiste en realizar un filtrado seguido a un submuestreo (Soman et al., 2010). Los filtros H_(z) y G_(z) guardan relación con las funciones ondita y escala seleccionadas para la construcción del análisis AMR. Mediante la selección de distintos pares de funciones ondita y escala, es posible construir distintos espacios AMR. Dicho algoritmo arroja como resultados 2 vectores de coeficientes: los coeficientes de detalles d[n] (que representan las componentes de alta frecuencia de la señal) y los coeficientes de aproximación c[n] (que representan los componentes de baja frecuencia de la señal) (Mallat, 2008).
Figura 3: Banco de filtros.
De esta manera, se obtiene una descomposición de la señal, en información de detalle y de aproximación, conservando la energía. Esta separación en detalles y aproximación guarda una relación con información de alta frecuencia (para los detalles) y de baja frecuencia (para las aproximaciones). Esto se puede observar en el algoritmo de banco de filtros de la Figura 3, donde la señal es filtrada por un filtro de alta frecuencia representado por H_[z] y un filtro de baja frecuencia representado por G_[z]. Esta asociación, con filtros de alta y baja frecuencia, está relacionada de tal modo que la función ondita -donde se realiza la proyección- es una señal de valor medio nulo, lo que puede asociarse a un sistema cuya respuesta no tiene componentes en baja frecuencia (filtro pasa altos). En contrapartida, la función escala es una función que sí tiene valor medio, por lo cual se lo puede asociar a un sistema que tiene respuesta en las bajas frecuencias (filtro pasa bajos).
Realizando una implementación recursiva de este algoritmo sobre los coeficientes de aproximación, se puede alcanzar un nivel de descomposición mayor y así ampliar la dimensión del hiperespacio. En cada nivel de descomposición alcanzado, la longitud de los coeficientes obtenidos se ve reducida a la mitad debido al submuestreo, por lo que el nivel máximo de descomposición posible de alcanzar guarda una relación diádica con la longitud de la señal original conforme a la expresión log2(N), siendo N la longitud de la señal en número de muestras.
Para reconstruir la señal en el dominio del tiempo, a partir de dichos coeficientes, se emplea el algoritmo inverso (síntesis). En la Figura 4 se puede observar el esquema del proceso de análisis (descomposición) y síntesis (reconstrucción), para dos niveles de descomposición.
Figura 4: Esquema del algoritmo de análisis y síntesis de TDO.
Se obtiene de este modo, un conjunto de señales r1(t), r2(t) y s2(t), pertenecientes al dominio del tiempo, donde cada una contiene información de cierta banda de frecuencias de la señal original s0(t). Al igual que en la Serie de Fourier, cada función de la base representa cierta banda espectral de la señal, con la ventaja de que la TOD brinda información tiempo-escala de la señal. Esto significa que la TOD no solo brindará información sobre qué componentes de frecuencia están presentes en la señal transformada, sino también en qué momento ocurren. De este modo, empleando distintas familias de onditas, para la generación de la base del AMR, se podrán encontrar distintas proyecciones, debiéndose utilizar aquella que ponga de manifiesto con mayor claridad la información de la señal que se desea obtener. A modo de ejemplo, se representa en la Figura 5 una descomposición de 2 niveles de un pulso de DP. La imagen superior izquierda presenta un pulso de DP del tipo interna, adquirido por el sistema de medición, junto al módulo del espectro en frecuencia de este (imagen superior derecha). En la segunda fila, se presenta la reconstrucción del detalle 1 que surge de la descomposición del mencionado pulso (izquierda), así como el módulo de su espectro en frecuencia (derecha). Observando tanto la información en el dominio temporal como en el dominio frecuencial, se hace notar que señal del detalle 1 no contiene información del fenómeno de DP que se desea estudiar. Lo mismo ocurre para la señal del detalle 2, obtenida de la descomposición del pulso bajo análisis. Para ambos detalles, se observa en el módulo del espectro en frecuencia, información en torno a los 150MHz (detalle 1) y 100MHz (detalle 2); valores muy superiores a la frecuencia de corte superior de 80MHz del sensor inductivo de alta frecuencia empleado para la adquisición del pulso. Finalmente, se tiene la señal de aproximación 2 (cuarta fila, sobre la izquierda) que surge de la descomposición de pulso de DP analizado mediante TOD, en conjunto con el módulo de su espectro en frecuencia (cuarta fila, sobre la derecha). Dada las características que presenta una descomposición del TOD, la señal de aproximación 2 se corresponde al complemento que necesitan las señales detalle 1 y detalle 2 antes mostradas, para reconstruir la señal original. De este modo, sumando las señales detalle 1, detalle 2 y aproximación 2 se puede reconstruir la señal original. Al notar que el detalle 1 y el detalle 2 se corresponde con ruido; se pueden descartar para el procesamiento de la señal de DP y así trabajar solamente con información que se corresponda con el fenómeno de DP (señal aproximación 2).
Figura 5: Descomposición en dos niveles del pulso tipo interno mediante db10.
En el presente trabajo se utilizó la TOD para descomponer señales de DP en diferentes señales de detalle y aproximación. A partir de estas, se calcularon parámetros adecuados para la conformación de un mapa de clasificación, capaz de discriminar fenómenos de DP proveniente de diferentes fuentes.
METODOLOGÍA
Fuentes de DP adquiridas
Las DP fueron adquiridas en laboratorio. Se desarrollaron probetas con características adecuadas para simular diferentes tipos de DP. Mediante una configuración de electrodos adecuada y un sistema de medición propio, desarrollado en la UTN FRGP (Maillot, 2015), se obtuvieron 3 tipos de fenómenos diferentes y también se registró ruido de 2 fuentes distintas. Todos ellos se listan a continuación:
- DP Interna en papel impregnado en aceite (configuración plano-plano).
- DP Interna en resina epoxy (configuración punta-plano, con el electrodo embebido en resina epoxy).
- DP Corona en aire A (alambre delgado en aire).
- DP Corona en aire B (punta-plano en aire).
- Ruido electromagnético obtenido en una estación transformadora de AT (dos fuentes de ruido).
Más detalles de los electrodos pueden encontrarse en (Maillot, 2017; Bonini et al., 2019). Para todos los casos, ninguna otra fuente de DP fue conectada durante cada ensayo individual, por lo cual se obtuvieron señales puras de DP para cada configuración. De esta manera, se relevó el conjunto de datos que se presenta a continuación:
|
DATO
|
CANTIDAD DE PULSOS
|
|
DP Interna papel
|
1.500
|
|
DP Interna epoxy
|
1.500
|
|
DP corona A
|
1.500
|
|
DP corona B
|
1.500
|
|
Ruido A
|
1.500
|
|
Ruido B
|
1.500
|
Tabla 1. Conjunto de datos de DP.
En la Figura 6, pueden apreciarse los patrones de DP y sus características estructurales obtenidas para tres configuraciones de electrodos adoptadas.
Figura 6: Patrones de pulsos de DP adquiridos correspondiente a diferentes fuentes.
Equipamiento y circuito de medición
En la Figura 7 se aprecia la configuración adoptada y los equipos utilizados para realizar los ensayos. Las características principales de dichos equipos se listan a continuación:
- Fuente de alta tensión de 40 kV, 2 kVA.
- Divisor de voltaje resistivo, relación 10.000:1.
- Capacitor de acoplamiento cerámico de 17 pF, 20 kV.
- Sensor inductivo de alta frecuencia 1-80 MHz, 15 mV/mA.
- Osciloscopio digital Agilent DSOX2024A.
Figura 7: Circuito de ensayo.
Para evitar ruido corona en las conexiones de alta tensión, las mismas fueron realizadas con caños de cobre de 12,5 mm de diámetro. Con el propósito de corroborar la ausencia de fenómenos indeseados, el sistema completo fue sometido a 20 kV, habiendo retirado previamente la probeta de la cuba de ensayos. Esto permitió corroborar la ausencia total de fuentes de DP, tanto en los equipos como en los elementos utilizados para su conexión.
Los pulsos fueron adquiridos a una tasa de muestreo de 500 MSa/s con una ventana temporal de observación de 2 us, por lo que cada pulso de DP adquirido tiene una longitud de 1.000 muestras. Cada pulso adquirido fue normalizado utilizando el operador norma cuadrada para la posterior etapa de procesamiento.
En la Figura 8 pueden apreciarse 3 pulsos de DP registrados bajo distintas probetas. Para los 3 pulsos mostrados, se observa un considerable aporte de ruido (como fuera comentado en la Figura 5) y diferencias estructurales en los pulsos de cada fuente. Estas diferencias se analizarán y caracterizarán en el dominio de la frecuencia mediante TOD, lo que permitirá desarrollar herramientas de procesamiento capaces de separar los pulsos provenientes de distintas fuentes.
Figura 8: Forma de onda de 3 pulsos adquiridos.
RESULTADOS
Los niveles de descomposición utilizados para el análisis fueron el nivel de aproximación 2 (c2) y los niveles de detalle 3 (d3), 4 (d4) y 5 (d5). El nivel de aproximación c2 se corresponde a señales sin la información del detalle 1 y del detalle 2 (ver en la Figura 5, el último gráfico de la aproximación 2), donde se observa claramente que la información eliminada (detalle 1 y detalle 2) se corresponde con ruido de alta frecuencia (superior a los 80MHz). Los detalles 3, 4 y 5, se corresponden a distintas bandas de frecuencias del pulso representado por la aproximación 2. La aproximación 5, fue descartada del análisis por contener bajos niveles de energía respecto de la energía total del pulso.
Una vez calculados los parámetros Vefc2, Vefd3, Vefd4 y Vefd5 con las expresiones (7) y (8); se proyectaron las combinaciones posibles de los mismos en un espacio de 2 dimensiones como muestra la Figura 9 y posteriormente se analizaron los grupos formados. Al tener individualmente identificadas las distintas fuentes que generan los pulsos de DP o ruido, es posible colorear cada grupo a fin de evaluar la capacidad de separación del mapa de clasificación propuesto.
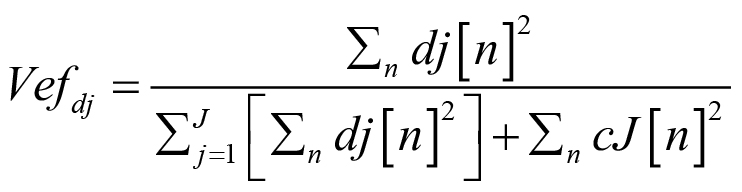
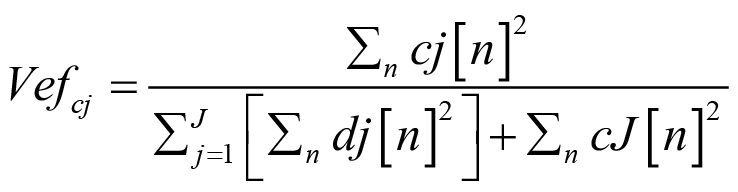
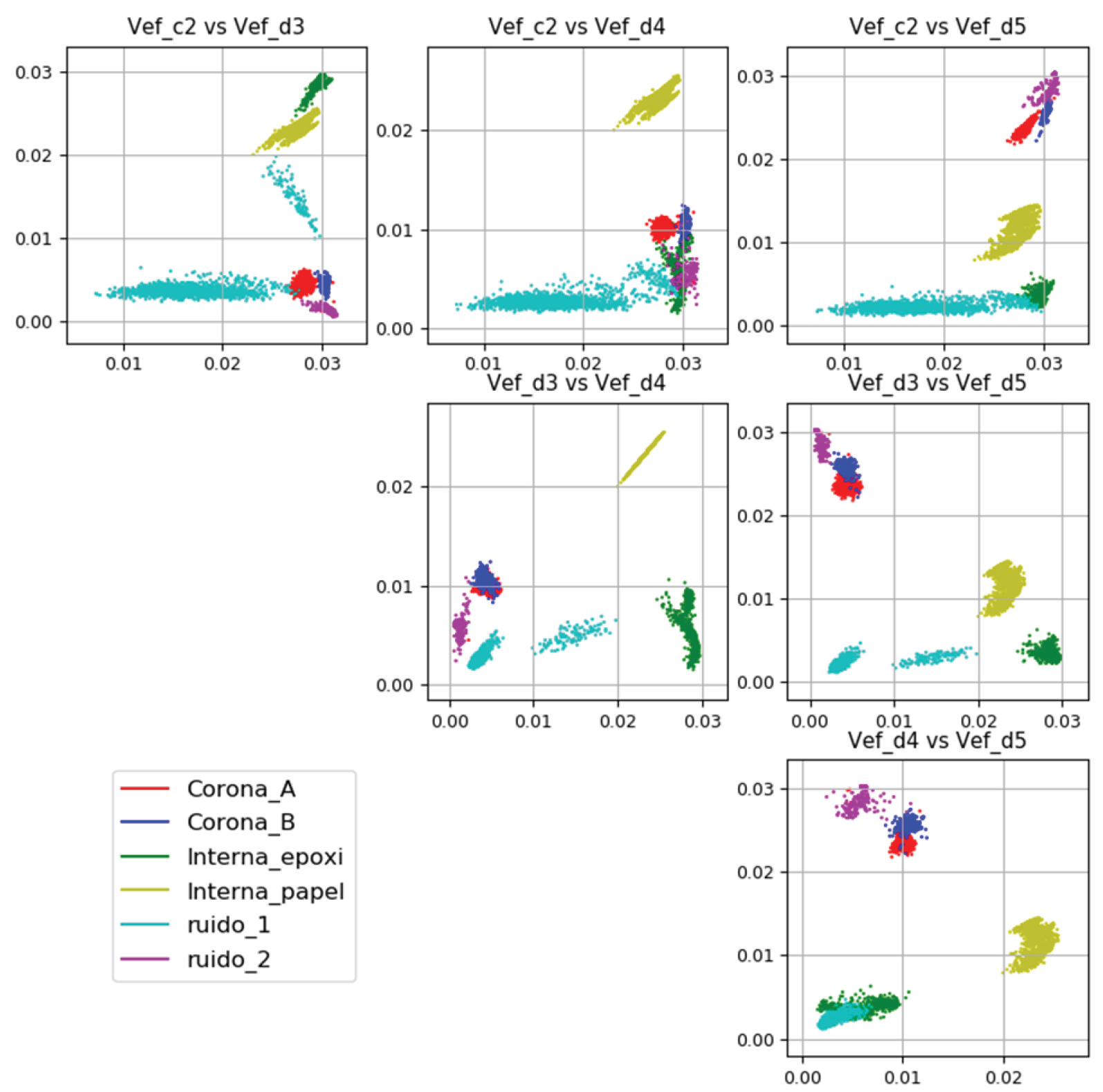
Figura 9: Proyección de la energía (Vef) de los coeficientes c2, d3, d4 y d5 para el conjunto bajo estudio.
Se presentan en la Figura 9 las proyecciones para el parámetro Vef de los pulsos de DP, analizados mediante la TOD. Se asignó un color a cada fuente individual procesada y se evaluó si cada nube de puntos puede ser aislada respecto de las otras. En la primera fila de imágenes, nos encontramos con el parámetro Vefc2 en el eje horizontal; contra los parámetros Vefd3 (primera columna), Vefd4 (segunda columna) y Vefd5 (tercera columna) en el eje vertical. Para estos casos, se observa que el parámetro Vefc2 no es capaz de separar ninguna fuente, ya que en la proyección de cada fuente sobre su eje resultaría en una conglomeración de puntos sin fronteras claras. En la segunda fila de imágenes, se presentan las proyecciones de Vefd3 en el eje horizontal contra Vefd4 (sobre la izquierda) y Vefd5 (sobre la derecha) en el eje vertical. Estas son las mejores proyecciones halladas para el parámetro Vef ya que el parámetro Vefd3 separa fácilmente las clases Interna_papel e Interna_epoxy (Vefd3>0,02) respecto de las demás clases (Corona_A, Corona_B, ruido_1 y ruido_2) si de Vefd3<0,01. Empleando el eje vertical de estas dos proyecciones y siguiendo un procedimiento de análisis similar, es posible hacer una separación más acabada del conjunto de fuentes.
Con reglas más complejas, es posible separar en las proyecciones Vefd3 vs Vefd4 y Vefd3 vs Vefd5 todas las clases bajo análisis, a excepción de las clases corona (azul y roja), ya que se encuentran mezcladas; pero esto no representa inconveniente ya que corresponden a un mismo tipo de defecto y pueden ser fácilmente separadas de las otras fuentes o ruidos.
Por último, la imagen de la tercera fila presenta en el eje horizontal la proyección de Vefd4 y en el eje vertical a Vefd5. Para este caso, la superposición de las clases Interna_epoxy con la clase ruido_1 nos llevó a descartar por completo esta combinación de proyecciones, ya que no permite aislar un tipo de DP crítico (interna) frente a ruido.
Como es sabido, cada nivel de descomposición de TOD se corresponde con una banda frecuencia del pulso original. Por esto, la capacidad de separar fuentes de DP empleando la energía o el valor eficaz de los niveles de descomposición, señala que la energía del pulso de DP para cada tipo se distribuye de cierta manera particular en el espectro en frecuencia. Teniendo presente la descomposición de la señal mediante filtros de alta y baja frecuencia -presentados en el algoritmo de banco de filtros- y considerando una descomposición teórica de la TOD, en la Tabla 2 se aprecian las bandas de frecuencia ideales para cada nivel de descomposición, teniendo presente la tasa de muestreo de 500MSa/s empleada para la adquisición de los pulsos.
|
NIVEL DE DESCOMPOSICIÓN
|
BANDA DE FRECUENCIA TEÓRICA (MHz)
|
|
d1
|
125 - 250
|
|
d2
|
62,5 – 125
|
|
d3
|
31,25 – 62,5
|
|
d4
|
15,625 – 31,25
|
|
d5
|
7,812 – 15,625
|
|
d6
|
3,906 – 7,812
|
|
c6
|
0 – 3,906
|
Tabla 2. Bandas de frecuencia ideales obtenidas para los diferentes niveles de descomposición.
En este sentido, se propone analizar la información espectral de dichos niveles de detalle. Para esto se utilizan las señales reconstruidas de cada nivel de descomposición empleando el algoritmo de bancos de filtros de reconstrucción presentado en la Figura 3 y, posteriormente, se calculan los siguientes parámetros (véase Tabla 3) pertenecientes al dominio de la frecuencia:
|
PARÁMETRO
|
DESCRIPCIÓN
|
|
Xmax
|
Valor máximo del módulo del espectro.
|
|
Fmax
|
Frecuencia de Xmax.
|
|
BW_3 dB
|
Ancho de banda de -3 db medidos desde del máximo del módulo del espectro.
|
Tabla 3. Parámetros pertenecientes al dominio de la frecuencia calculados a cada señal reconstruida.
A continuación, se calcularon estos parámetros a las señales reconstruidas correspondientes para los niveles c2, d3, d4 y d5 de cada pulso de DP. Seguido esto, se realizó para cada parámetro, la proyección de la combinatoria de los valores hallados en cada nivel de descomposición, al igual que en la Figura 9 para Vef. Esto permitió evaluar la capacidad de los nuevos parámetros para discriminar pulsos provenientes de fuentes diferentes. Solo se encontraron resultados favorables empleando el parámetro Xmax; estos se muestran en la Figura 10.
Figura 10: Proyección del máximo del espectro (Xmax) de la energía en los coeficientes d3, d4 y d5 para el conjunto bajo estudio.
Se presenta en la primera fila de imágenes, la proyección del parámetro Xmax_c2 en el eje horizontal contra Xmax_d3 (primera columna), Xmax_d4 (segunda columna) y Xmax_d5 (tercera columna) en los respectivos ejes verticales. Para los tres gráficos, se observa que no hay una regla eficaz de separación sobre el parámetro Xmax_d2 dado que la proyección de los puntos sobre este eje generaría una superposición de todas las clases. En la segunda fila de imágenes, se presenta Xmax_d3 en el eje horizontal contra Xmax_d4 en el eje vertical para la imagen de la izquierda, y contra Xmax_d5 en la imagen de la derecha. Se observa una muy buena capacidad de separación, aún para la clase ruido_2 con las respectivas coronas, ya que la clase ruido_2 presenta una alta densidad de puntos en la coordenada Xmax_d4≈4 o Xmax_d5≈15, que permite diagramar una frontera que la separe de las clases corona.
La imagen de la tercera fila presenta a los parámetros Xmax_d4 en su eje horizontal y a Xmax_d5 en el eje vertical. Aquí la clase interna_epoxy (color verde) se encuentra totalmente cubierta por la clase ruido_1 (color cyan), lo que nos lleva a descartar esta proyección por el mismo motivo expuesto anteriormente.
Respecto del parámetro anterior Vef (Figura 9), para la proyección Xmax_d3 vs Xmax_d4 o Xmax_d3 vs Xmaxd5, se observa un pequeño detrimento en la capacidad de separar las fuentes, ya que las nubes se encuentran algo más próximas respecto del anterior. Cabe destacar de este gráfico, la similitud de la ubicación de cada nube de puntos respecto del gráfico anterior (Figura 9); señalando esto: que existe cierta proporcionalidad entre la energía de dichas señales y el valor máximo de su espectro.
Este último hallazgo nos llevó a analizar el espectro del pulso sin realizar descomposición de TOD con este mismo parámetro y en las bandas de frecuencia señaladas en la Tabla 2. Para esto, se halló el espectro del pulso original y se buscaron los máximos en las bandas de frecuencia correspondientes a los niveles c2, d3, d4 y d5. En la Figura 11, se muestran los resultados del mapa de clasificación generado a partir de dicho parámetro para cada banda de frecuencia e identificados con las variables max_c2, max_d3, max_d4 y max_d5, respectivamente.
Figura 11: Proyección del máximo del espectro (max) para las bandas c2, d3, d4 y d5 señaladas en la Tabla 2.
En la Figura 11, se presentan la combinación de parámetros para las bandas c2, d3, d4 y d5 al igual que en las figuras 9 y 10 pero, en este caso, el parámetro empleado es el valor máximo de su espectro en dicha banda. Para la primera fila de imágenes, donde se presenta en el eje horizontal el max_c2, se observa que este parámetro no aporta información que permita separar fuentes.
La imagen de la tercera fila, max_d4 en eje horizontal y max_d5 en eje vertical, conserva el comportamiento de superposición entre clases Interna_epoxy (verde) y ruido_1 (cyan), motivo por el cual esta proyección debe ser descartada.
Por último, de las imágenes de la fila central, donde se representa en el eje horizontal max_d3, solo se pueden separar las clases en la imagen de la derecha con max_d5 en el eje vertical, ya que las clases corona está separadas de la clase ruido_2 debido a que existe una alta densidad de puntos de esta clase en torno a max_d5 ≈ 0.032 que permite vislumbrar una frontera.
Al comparar con la Figura 9, se observa una merma en la capacidad de separación, siendo ahora solamente posible separar las fuentes en la proyección max_d3 vs max_d5. Esta pérdida se puede ver compensada en un menor requerimiento de cómputo, ya que para este caso solo fue necesario realizar una normalización del pulso, seguida de la transformada rápida de Fourier y la búsqueda de los máximos entre ciertas bandas fijas. La simplicidad en el procesamiento permite una implementación en línea del algoritmo con menor costo computacional que las involucradas en la TOD, donde cada nivel de descomposición implica un producto de convolución con 2 filtros, seguido de un submuestreo.
De esta manera, queda demostrado que es posible separar fuentes de DP empleado los máximos de las bandas de frecuencia del detalle d3 y del detalle d5 para una tasa de muestreo de 500 MHz. En la siguiente sección, se emplea esta técnica para separar un patrón de DP mezclado obtenido de un equipo eléctrico en operaciones.
Aplicación experimental
Para probar la técnica propuesta, se tomaron mediciones en un transformador de corriente (TI) de 33 kV aislado en papel impregnado en aceite con DP del tipo interna (Maillot et al., 2014) al cual se le incorporó un alambre vertical conectado a una de sus partes activas para producir DP corona. Adicionalmente, se agregaron a los datos adquiridos: ruido electromagnético y DP corona, adquiridas en laboratorio. En la Figura 12 se presenta el patrón mezclado, compuesto por las distintas fuentes antes mencionadas, donde resulta muy complejo emitir un diagnóstico sobre el tipo de DP presente en la medición. En la Figura 14, se muestra el mapa de clasificación de los pulsos adquiridos empleando la operación max_d3 vs max_d5 propuesta en este trabajo y seleccionando de forma manual distintos grupos de pulsos.
Figura 12: Patrón adquirido sobre equipo real.
Figura 13: Patrón adquirido sobre equipo real y su mapa de clasificación correspondiente. Colores resultantes de una selección manual de los grupos.
En el mapa de clasificación formado, se pueden seleccionar manualmente distintos grupos de puntos, basándose en la proximidad o densidad de puntos por unidad de superficie y asignando un color de identificación a cada uno de estos grupos. De esta manera, se observan 4 grupos bien definidos por su densidad (subpatrón 1 a 4; verde, rojo, azul y amarillo respectivamente) y una dispersión general de puntos (subpatrón 5, cian) que surge de los puntos no seleccionados en los 4 grupos anteriores (ver Figura 14). Para los subpatrones 3 y 4, se pueden distinguir las fronteras al aumentar la escala en dicha área, que en la escala representada no es posible distinguir debido al espesor de las marcas utilizadas.
Figura 14: Subpatrones resultantes de los grupos de pulsos marcados en la Figura 13.
Se puede identificar, en el subpatrón número 1, un patrón característico de ruido corona, por tener actividad centrada en los máximos de la senoide de referencia. Para el caso del subpatrón 2, este se corresponde con ruido electromagnético por no guardar correlación con la fase. En el subpatrón 3 se encuentra actividad de DP de tipo interna por tener actividad concentrada en el primer y tercer cuadrante, mientras que el subpatrón 4 coincide con DP corona por tener actividad centrada en el máximo de la tensión de referencia. Este último, al tener única polaridad, se trata del efecto punta producido por el alambre incorporado al TI bajo ensayo, conforme fue presentado en (Maillot et al., 2014). Por último, en la colección de puntos dispersos correspondiente al subpatrón 5 se puede observar que estos se mezclan con los dos anteriores, subpatrones 3 y 4, demostrando así que dichos 2 grupos presentan características semejantes para el espacio de características propuesto, por lo tanto, se encontraban más mezclados que las otras clases.
Por último, cabe mencionar la necesidad de poder aplicar este algoritmo a más fuentes de señales de DP o a más mediciones sobre equipos reales, con el empleo de distintos tipos de sensores para poder generalizar y revalidar los resultados encontrados.
CONCLUSIONES
En este trabajo, se presentó una novedosa herramienta de caracterización de señales provenientes de ensayos de DP, con el objeto de obtener un mapa de clasificación donde señales de distintos orígenes puedan ser individualizadas. Para esto, se partió de trabajos previos donde se empleaba la energía de diferentes niveles de descomposición obtenidos con la TOD y la técnica de PCA o mapas autoorganizados, para realizar una reducción de dimensiones.
Para independizarse de las distintas rotaciones que las técnicas de reducción de dimensiones involucran, según cada conjunto de datos a analizar, se estudió la proyección directa de distintos parámetros propuestos en 2D. En este sentido, se compararon los mapas de clasificación de las combinaciones posibles entre los niveles de descomposición c2, d3, d4 y d5 encontrando resultados positivos. Esto permitió estudiar los sectores del mapa de clasificación que se corresponden con cada fuente de DP, de forma independiente a los datos que se emplean.
Siguiendo en esa línea, se procedió a evaluar si los parámetros de la información espectral de cada nivel de descomposición presentados (Xmax, Fmax, BW_3_db) eran capaces de cumplir con tal objetivo. Se encontró que mediante el parámetro Xmax (valor máximo del espectro) fue posible separar los pulsos de DP provenientes de diferentes fuentes de manera aceptable. Seguidamente, se estudió qué ocurría si se calculaba el mismo parámetro, pero sobre el pulso sin descomponer con TOD, en las bandas de frecuencia ideales de cada nivel de análisis. Se encontró una merma en la capacidad de separación de fuentes, pero se la puede considerar compensada por el hecho de demandar un menor procesamiento de datos, facilitando esto la implementación en línea de dicho algoritmo.
Los hallazgos en este trabajo permiten afirmar que, con un algoritmo de simple implementación y muy bajos recursos computacionales, es posible separar fuentes de DP en sistemas en línea de monitoreo y medición. Para poder implementar esta metodología de procesamiento, es necesario contar con un sistema de medición que tenga una respuesta en frecuencia aproximadamente lineal para las bandas de frecuencia a procesar (entre 7 y 63 MHz), de modo tal que la información conserve su proporcionalidad y pueda implementarse está técnica.
REFERENCIAS
Bonini, C. y Enciso, L. (2015). “Caracterización de patrones de Descargas Parciales internas y superficiales mediante ensayos de laboratorio”. 1er Congreso de Investigación y Transferencia Tecnológica en Ingeniería Eléctrica. Gral. Pacheco. Argentina. 16 al 18 de septiembre.
Bonini, C.; Pesana, F.; Maillot M. (2019). “Detecting deterioration stages in epoxy resins specimens under partial discharge process”. Journal of Electrical Engineering. Vol. 7. 2019. págs. 39-50.
Cavallini, A.; Conti, M; Montanari, G. C. y Conti, A. (2002). “Indexes of the Recognition of Insulation System Defects Derived from Partial Discharge Measurements”. IEEE International Symposium on Electrical Insulation. Boston, Estados Unidos. 7 al 10 de abril.
Cavallini, A.; Conti, A; Montanari, G. C. y Puletti, F. (2003a). “Advanced PD Inference in On-Field Measurements. Part 1: Noise Rejection”. IEEE Transactions on Dielectrics and Electrical Insulation 10.2, págs. 216-224.
Cavallini, A.; Conti, A.; Conti, M y Montanari, G. C. (2003b). “Advanced PD Inference in On-Field Measurements. Part 2: Identification of Defects in Solid Insulation Systems”. En: IEEE Transactions on Dielectrics and Electrical Insulation. Vol 10, nro.3, págs. 528-538.
CIGRE WG D1.37 (2016). “Guidelines for partial discharge detection using conventional (IEC 60270) and unconventional methods”. Technical Brochure 662 CIGRE.
Gulski, E. y Kreuger, F. (1992). “Computer-aided recognition of Discharge Sources”.
En: IEEE Transactions on Dielectrics and Electrical Insulation. Vol. 27. Nro.1, págs. 1702-1711-55.
Hao, L.; Contin, A.; Hunter, J.; Swaffield, D. J.; Lewin, P. L.; Walton, C.; y Michel, M. (2011). “A new method for automatic Multiple Partial Discharge Classification”. XVII International Symposium on High Voltage Engineering, Hannover, Germany, 21 al 25 de agosto.
IEC 60034-27-2. (2012). “Rotating electrical machines - Part 27-2: On-line partial discharge measurements on the stator winding insulation of rotating electrical machines”. Edición 1.
IEC 60270. (2002). “High-voltage test techniques – Partial discharge measurements”. Edición 3.
IEEE C37.301. (2009). “IEEE Standard for High-Voltage Switchgear (Above 1000 V) Test Techniques - Partial Discharge Measurements”.
Kreuger F. H., Gulski E. y Krivda A. (1993). “Classification of Partial Discharges”. IEEE Transactions on Electrical Insulation. Vol. 28 No. 6.
Jiang, L.; Jiang, T.; Harrison, R. F.; y Grzybowski, S. (2012). “Recognition of ultra-high frequency partial discharge signals using multi-scale features”. IEEE Transactions on Dielectrics and Electrical Insulation, vol. 19, no. 4, pp. 1412-1420.
Maillot M., Bonini C., Enciso L., Galliani M., Rivera O. y Casas R. (2014). “Incorporación de la medición de Descargas Parciales on-line como herramienta de diagnóstico”. CIDEL 2014 Congreso Internacional de Distribución Eléctrica. Buenos Aires. Argentina. 22 al 24 de septiembre.
Maillot, Bonini, Enciso y Galliani. (2015a). “Experiencias de laboratorio en medición de Descargas Parciales sobre Transformadores de Corriente de aislación papel-aceite”. XVI ERIAC (Encuentro Regional Iberoamericano del CIGRE). Foz du Iguacu, Brasil. 17 al 21 de mayo.
Maillot, M. (2015b) “Desarrollo de un equipo de medición de descargas parciales para monitoreo, investigación y diagnóstico”. 1er Congreso de Investigación y Transferencia Tecnológica en Ingeniería Eléctrica. Gral. Pacheco. Argentina. 16 al 18 de septiembre.
Maillot, M. (2017). “Comparison of feature space formation based on DWT coefficient variance for partial discharge classification under different wavelet families”. 20th International Synopsium on High Voltage Engineering. Buenos Aires. Argentina. 28 de agosto al 1 de septiembre.
Maillot, M. y Pessana, F. (2018). “A new feature space for partial discharge signal separation based on DWT coefficient variance”. Journal of Electrical Engineering. Vol. 6. 2018.
Maillot, M.; Bonini, C.; Enciso, L. (2019). “Herramientas de clustering automático de señales para la medición de descargas parciales”. Tercer congreso de investigación y transferencia tecnológica en Ingeniería Eléctrica (CITIE). La Plata, Buenos Aires, Argentina. 13 al 14 de septiembre.
Mallat S. (2008). A Wavelet Tour of Signal Processing. Third Edition: The Sparse Way. Academic Press.
Mor, A. R. “Nueva metodología de la medida de descargas parciales en cables de alta tensión”. Tesis (Doctor en ingeniería). ITE. Valencia, España. 277 pág. (2012).
Paoletti G. J, Golubev A. (2001). “Partial Discharge Theory and Technologies Related to Medium-Voltage Electrical Equipment”. IEEE Transactions on industry applications, vol. 37, No. 1.
Salcedo J., Degl’Innocenti A. (2001). “Sistema Predictivo Aplicado al Mantenimiento de Estaciones Transformadoras”. IX ERIAC (Encuentro Regional Iberoamericano del CIGRE). Foz do Iguaçu – Brasil. 11 al 24 de mayo.
Soman, K. P.; Ramachandran, K. I. y Resmi, N. G. (2010). Insight into waveletes. From
theory to practice. (3ra edición). PHI Learning.
Sirne, R. O. y C. E. D’Attellis (2004). Introducción a Onditas, con aplicación a la Caracterización Frecuencial del EEG. Centro de Procesamiento de Señales e Imágenes.
Wu, M.; Cao, H.; Cao, J.; Nguyen, H.; Gomes, J. B.; y Krishnaswamy, S. P. (٢٠١٥). “An Overview of State-of-the-Art Partial Discharge Analysis Techniques for Condition Monitoring”. IEEE Electrical Insulation Magazine, Vol. 31, No. 6.
(1)
(2)
(3)
(4)
(5)